定制小分子力场(七)：金属离子参数拟合

Posted on 2024-11-26

离子参与大量的生物学反应过程，PDB数据库中几乎超过40%的蛋白结构都含有金属离子。特别是二价金属离子，在生物大分子的结构，催化，电子转移过程中行使重要功能。金属离子的力场参数相比生物大分子或有机小分子的力场参数更简单，因此在模拟过程中往往被忽略，但错误的使用过时的、不合理的力场参数，会导致模拟过程中的能量、结构累积误差，最终导致错误的结论。因此，本文将以生物体系的金属离子参数为主题，讨论离子参数的分类，拟合，和应用场景，为读者指出不同金属离子力场的正确使用策略。

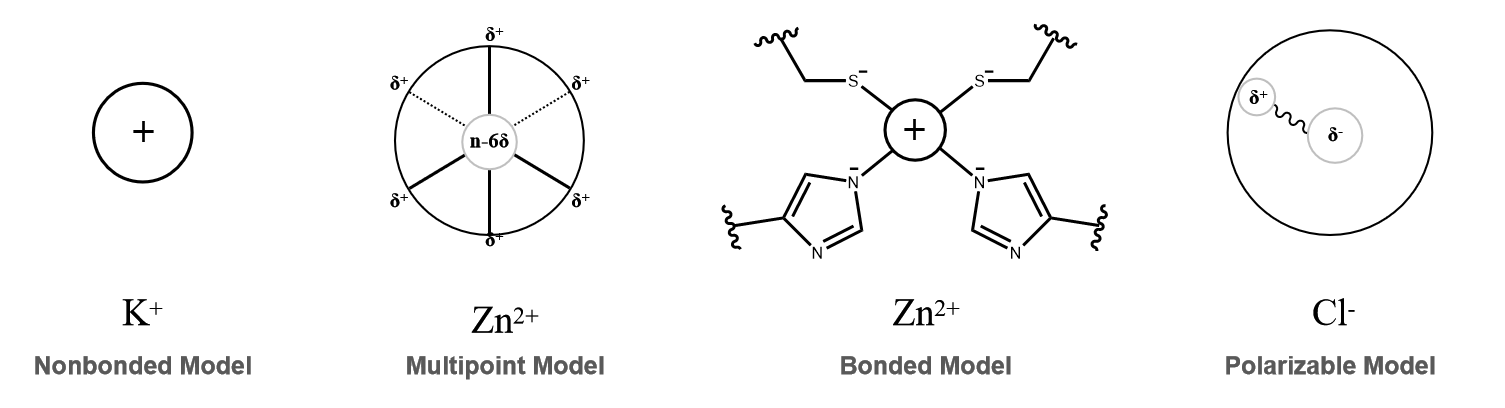
Ions Models

图7.1 常见离子模型

金属离子参数类型

分子模拟中的离子模型的参数根据模型的架构模式，常见的金属离子模型可以分为非键模型，成键模型，杂化模型，约束非键模型，哑原子阳离子模型，以及可极化模型。
下面简单描述下这几类离子模型的特征和适用场景，由于作者主要在生物医药领域工作，例子局限在工作领域内，难免有遗漏。

非键模型
非键模型，使用Lennard-Jones (LJ)所表述的范德华作用，以及Coulomb表述的库仑作用，来描述离子模型的方法。常见的范德华参数有12-6形式，也有使用12-6-4形式。离子模型可以通过采用12-6-4形式的参数以获得更好的极化效应。非键模型是目前大多数通用全原子力场的默认组成，比如GROMACS或AMBER软件包中大部分全原子力场中使用的离子力场。这种描述方法简单，计算快速，力场间的可迁移性强，因此广泛应用在各类生物，化学，以及材料行业中的模拟计算中。
成键模型
成键模型直接在离子和配位分子间定义成键参数（键长，键角，二面角），来描述金属复合物结构。使用成键参数的优势在于模拟过程中稳定保持金属螯合物结构，如铁-卟啉、人碳酸酐酶催化位点的锌离子核等，都可以使用这种模型。
杂化模型
杂化模型对离子和配体之间的相互使用成键和非键参数混合进行描述，保证结构稳定性的同时兼顾非键作用参与作用的配体。如Chakravorty和Merz等人在金属伴侣蛋白CusF蛋白的金属簇描述中，对N(His)-金属离子(Cu+/Ag+)-S(Met·2)的作用进行成键参数描述，对与金属离子形成阳离子-pi相互作用的Trp作用进行非键参数描述。由Pengfei Li和Kenneth M. Merz Jr等人开发的AMBER软件包中的MCPB.py模块可以自动完成此种方法的建模。
约束模型
与杂化模型类似，约束模型只是不使用成键参数固定金属离子和配体间的相互作用，而是替换为距离或角度约束(constrants)。这种方法相比使用成键参数，所需拟合的参数仅仅是平衡长度，不再需要力常数。该方法也被广泛应用在金属蛋白模拟中。
多点电荷模型
多点电荷模型，或哑原子阳离子模型，是一种在点电荷模型上添加哑原子，仅使用非键参数来描述阳离子和配体(水或残基)间配位的方法。常见的哑原子模型以正八面体的结构搭建，其中阳离子参数位于中心，哑原子参数则位于各个顶点。如Zn²⁺离子在水中会和8个水分子形成螯合，所以可以使用正八面体分布的哑原子描述Zn²⁺离子，以模拟形成配位相互作用时存在构象偏好。哑原子阳离子模型的哑原子一般带正电，阳离子本身带少量正电荷、0电荷、甚至负电荷，来模拟正电荷分布在离子表面。使用哑原子阳离子模型，相比单点非键模型相比，更能准确描述离子和配体间的几何排布及能量，在Zhang等人的研究中，只有使用多点Ca²⁺离子模型时能够模拟RyR1阳离子通道中的Ca²⁺转运过程，而单点Ca²⁺离子模型则无法穿过该离子通道。
可极化模型
可极化模型描述的离子即可极化离子，常见的极化模型包括Drude震荡子模型(Drude Oscillator Model, DO)，诱导偶极模型(Induced Dipole Model, IDM)和震荡电荷模型(Fluctuating Charge Model, FQ)。DO模型是Drude于1902年提出的一种用于描述金属中电子与电磁场相互作用的经典物理模型。DO模型通过在原子上添加一个弹簧(或轻杆)链接一个Drude电荷(偏电荷)。Drude电荷在模拟过程中随着环境发生电荷偏移，从而产生多变的瞬时偶极。DO模型最早在20世纪50年代就应用在金属离子的固相或液相体系的模拟，后续也逐渐扩展到有机小分子甚至生物大分子领域，比如使用DO模型描述I^-离子的易极化特性等。同样地，使用FP模型或DO模型的Cl^-离子时，Cl^-离子会倾向于排布在溶剂表面，而非极化模型则没有此现象，Stuart和Berne认为极化模型下的表面分布行为可能与Cl^-离子的“结构破坏”效应相匹配。使用IDM模型相比非极化模型，对阳离子-π(Cation−π)相互作用有较大的提升，尽管由于阳离子-π存在“电荷转移效应(Charge Transer)”的存在，目前任何力场模型都不能完美描述这一作用。Sakharov和Lim使用IDM模型描述锌蛋白的Zn-S(Cys^-)，能够极大地稳定这一结构。常见的IDM力场有AMBER ff02.pol，OPLS-AAP/CM1AP，AMOEBA，PFF，CTPOL等。

金属离子参数在拟合什么

非键参数拟合

Åqvist和Warshel等在1990年使用非键模型拟合Ca²⁺，Mn²⁺，Ba²⁺等二价阳离子参数时，认为拟合出的力场参数必须满足葡萄球菌核酸酶（Staphylococcal Nuclease, SNase）的催化动力学，即催化反应过程中的能垒。为了拟合这一过程，论文中巧妙地将酶促反应过程按照"经验价键模式"(Empirical Valence Bond, EVB)进行拆解，在使用FEP/MD方法计算Ca²⁺和Mn²⁺及Ba²⁺之间在结合SNase时进行Alchemical转换时的能量变化ddG，来判断离子非共价参数的稳定性。这里的共价参数是Lennard-Jones (LJ)所表述的范德作用，因为单点阳离子模型的库仑参数就是它本身的净电荷。

经过多年的发展和讨论，拟合通用离子模型时通常会在适配多种水模型，大分子力场的前提下，尽量使得拟合出的离子参数可以复现离子的重要宏观特征，如溶剂化能(Hydration Free Energies, HFEs)，离子-氧距离(Ion-Oxygen Distances, IODs)，水坐标数(Coordination Numbers, CNs)，晶格能(Lattice Energies)，晶格常数(Lattice Constants)。对于一个简单的12-6 LJ模型描述的单点离子模型，只需要拟合 $\sigma$ 和 $\epsilon$ 两个即可。

那么初始的 $\sigma$ 和 $\epsilon$ 参数如何获取呢？对于双参数优化，一种方法是给一个较大的范围进行系统搜索，比如Merz等人使用过这样一组参数进行系统搜索： $\sigma$ 在0.3 ~ 2.5 Å，间隔0.1 Å， $\epsilon$ 在1e-6 ~ 1.0 Å，间隔10倍，总计23 x 7 = 161种不同的参数组合。但是随之而来的问题是，不同的 $\sigma$ 和 $\epsilon$ 是可以获得完全相同的LJ势能面的，这是因为LJ函数中的 $A_{ij}=\epsilon_{ij}\sigma^{12}_{ij}, B_{ij}=\epsilon_{ij}\sigma^{12}_{ij}$ 两个参数由 $\sigma$ 和 $\epsilon$ 协同决定，因此一个 $\sigma$ 和 $\epsilon$ 参数组合与另一个稍小的 $\sigma$ 和稍大的 $\epsilon$ 参数组合所计算的LJ势能面是完全相等的。此时问题变为了解决LJ参数的唯一性问题。

这一问题的解决方法有多种。第一类方法，即单参数固定法，是固定 $\sigma$ 或 $\epsilon$ 中的一个参数，扫描另一个参数。比如Jensen和Jorgensen在OPLS中将阳离子的 $\epsilon$ 固定为 $0.0005 kcal/mol$ ，将阴离子的 $\epsilon$ 固定为 $0.71 kcal/mol$ 。又如Wo等人使用荷电壳(Charged Shell)半径和溶剂壳(Hydration Shell)半径通过经验公式计算获得计算 $\epsilon$ ，再通过 $\epsilon$ 计算 $\sigma$ 。第二类方法，双参数协同优化法，是通过优化过程中的 $\sigma$ 和 $\epsilon$ 的函数关系，将两参数问题降维到单参数问题。比如通过系统搜索方法，Merz等人发现在拟合宏观测量得到HFEs，IODs或CNs时，离子的 $\sigma$ 和 $\epsilon$ 程一定的数学关系（类似量化的Slater函数），他们叫这个相关曲线为理想气体曲线(Nobel Gas Curve, NGC)。因此可以仅扫描 $\sigma$ ， $\epsilon$ 直接套用NGC进行计算的方法计算。另外，在优化溶剂相参数后，同时考虑凝固相特征，如LEs和LCs的匹配情况进行参数选择，也可以缩小参数范围。

\epsilon = 0.063 \sqrt{r/\Delta r} \space\space\space\space\space (Won)

\epsilon = 57.36 \times e^{-2.471\times \sigma_{min}/2} \space\space\space\space\space (NGC)

接下来讨论离子参数拟合时考虑的宏观量是如何计算的。溶剂相的HFE，IOD，NC都可以通过实验手段计算。离子的HFE一般通过Alchemical Free Energy方法进行计算，即自由能微扰(FEP)或热力学积分(TI)方法。IOD和NC则通过常规的NPT模拟计算，NC可以直接通过统计第一壳层的水分子数量计算，IOD则通过计算水分子的O原子相对离子的径向分布函数(Radial Distribution Functions, RDFs)计算。以Merz工作流程为例，文章首先搭建多种水模型下（TIP3P, TIP3P-FB, OPC3, SPC/E, TIP4P_EW, OPC）的离子溶剂化体系，即一个(46Åx46Åx46Å)大小的PBC水盒子(约2,400水分子)中放入一个Dummy原子。对于HFE，经过NVT和NPT平衡后进行步长为1 fs的TI计算。TI变化拆分为VDW变化和ELEC变化阶段，VDW变化阶段使用3个窗口，COUL变化使用9个窗口。LJ势使用Soft-core缩放方法，ELEC使用PME计算长程静电势。对于IOD和NC，经过NVT和NPT平衡后进行步长为1 fs的10ns NPT模拟，每0.5 ps记录一帧体系坐标，模拟过程中使用PME计算长程相互作用，弱相互作用截断距离为10Å。模拟轨迹使用Kirkwood−Buff积分计算RDF，进一步即可得IOD和NC。HFE，IOD，NC等特性有时无法用单一参数同时兼顾，因此在Mertz等人的论文中会针对HFE和IOD进行专一性的优化，也有兼顾HFE和IOD的折中(ComproMise, CM)模型。

Table 7.1. 生物体系常用离子实验测得参数

ions	HFE(kcal/mol)	CN(#)	IOD(Å)
Li⁺	-113.5	4-6	2.08 ± 0.06
Na⁺	-87.2	4-8	2.35±0.06
K⁺	-70.5	6-8	2.79 ± 0.08
Ca²⁺	-359.7	8	2.46
Zn²⁺	-467.3	6	2.06 ± 0.01
Mg²⁺	−437.4	6	2.09 ± 0.04
Mn²⁺	−420.7	6	2.19 ± 0.01
Cu²⁺	-480.4	6	1.96 ± 0.04
Fe²⁺	-439.8	6	2.11 ± 0.01

HFE实验值引自 Marcus, Y. J. Chem. Soc., Faraday Trans. 1991, 87, 2995−2999.

这里给出Merz的Zn²⁺单点非键力场参数：

代码 7.1. Zn²⁺单点非键力场参数 GROMACS和AMBER力场格式

# Amber Format
# ion         r_d(A)   epsilon(kcal/mol)
Zn2+          1.271 0.00354287      JTTC,9,6,2733 (2013) CM TIP3P
Zn2+          1.455 0.02662782      JCTC,10,289, (2014)  TIP3P
Zn2+          1.280 0.00374505      JCTC,16,4429, (2020) CM OPC3



# Gromacs Format
# ion         sigma(nm)   epsilon(kJ/mol)
Zn2+          2.26466e-1 0.01482343      JTTC,9,6,2733 (2013) CM TIP3P
Zn2+          2.59251e-1 0.11141080      JCTC,10,289,  (2014)  TIP3P
Zn2+          2.28070e-1 0.01566929      JCTC,16,4429, (2020) CM OPC3

成键模型拟合

成键模型诞生之初就是为了金属蛋白的模拟，也能应用在类似领域比如金属有机框架(Metal-Organic Frameworks, MOFs)等。使用成键模型的金属-生物大分子复合物在整个模拟过程中都不会发生巨大的构象变化，可以用于研究酶促反应过程中的各种现象。目前最流行的成键参数拟合的方法是Li和Merz基于AMBERTOOLS开发的MCPB.py，可以较为简单地构建金属-蛋白复合的共价参数。

MCPB.py方法参数拟合可分为以下几步。1. 确定金属离子周围配位残基/或有机小分子片段形成的簇结构，对这一簇结构进行切除并封端；2. 使用量化软件，如GAUSSIAN或GAMESS-US，对不同大小簇模型的结构选择合理的优化策略进行构象优化；3. 对配位残基的进行两步RESP电荷拟合，可选策略包括全电荷拟合，氢原子拟合，侧链拟合等；4. 对金属-配位残基间的共价参数进行拟合，可使用Seminario或Z-matrix方法，对Zn²⁺离子可直接使用经验参数；5. 检查并补全缺失参数，拼合其余不参与拟合部分的参数，导出最终的AMBER格式拓扑和坐标文件；6. (可选)转化AMBER格式为GROMACS或LAMMPS或CHARMM格式。

多点非键参数拟合

在生物大分子如金属蛋白的模拟中，非键单点离子模型主要问题在于无法维持和蛋白配位时的几何结构。尽管共价/杂化能够刚性地维持金属-生物大分子间的几何结构，但是共价/杂化模型参数复杂，力场迁移性差，无法研究离子的解离过程，限制了它的使用范围。因此非键的多点模型被认为能够即保证一定的空间结构，也不引入刚性的共价参数。

多点模型的一般结构是一个位于中心的金属离子M，和分布在金属离子荷电壳层的哑原子D。D会分担一定的金属离子所携带的正电荷，因此需要将D均匀分布在金属离子的球面。又因为金属离子和水以及蛋白配位时具有一定的空间结构，比如前文中提到Zn²⁺的IOD等于6，因此可以将M放在正八面体的中央，D放在正八面体的6个顶尖。同理Ca²⁺的IOD等于8，可以使用正八面体(6顶尖)或者十面体(双五角锥/双正五角锥)(8顶点)。

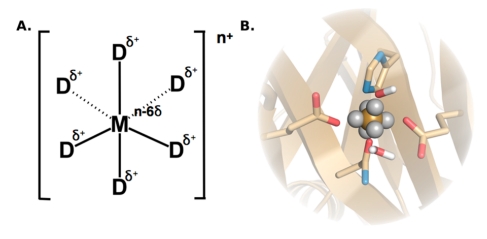
MutipointIonModel

图7.2 多点离子模型

相比单点离子模型，多点离子模型需要拟合的参数从2个LJ参数扩展到7+N个（以正八面体为例），其中7个是：M和D的距离d_M-D，D携带的电荷Q_D，M的 $\sigma_M$ 和 $\epsilon_M$ ，D的 $\sigma_D$ 和 $\epsilon_D$ ，D的质量m_D。其他N个参数可以通过这6个参数计算获得，比如M携带的电荷，和维持正八面体所需的D-D距离，D-M-D角度等。D围绕M旋转是允许的。最初的参数初猜同样来自Åqvist和Warshel等1990年的文章，在这篇文章中，针对Mg²⁺离子，Åqvist和Warshel等将6个哑原子D全部设置为仅携带Q_D电荷的库仑势点，中心金属离子M则是范德华势和静电势点，因此该模型仅需扫描 $\sigma_M$ ， $\epsilon_M$ ，d_M-D和Q_D四个参数。

Oelschlaeger等人，Saxena和Sept等人在后续的类似工作中也按照这一思路，只是将哑原子的范德华势能的斥力部分和哑原子质量也引入，即拟合6个参数，以保证其他分子不会过于靠近离子的哑原子。Duarte等人更是按此思路对多种过度二价金属进行了多点模型参数化。5参数形式的好处在于减少哑原子与其他分子过近的问题，但是缺点也明显：Buckingham形式的范德华参数在仅有斥力的C12参数下，使用时需要对模拟引擎进行调整适配。比如AMBER模拟引擎编译后力场参数文件中是Buckingham形式，因此只需手动修改参数；但GROMACS参数存储主要使用 $\sigma$ 和 $\epsilon$ 形式，且改gmx grompp编译出的力场参数文件.tpr文件是二进制文件，修改门槛较高。也可以手动将所有原子类型和哑原子的非键作用使用Buckingham形式[nonbond_parms]直接强制定义，虽然繁琐但确可行。

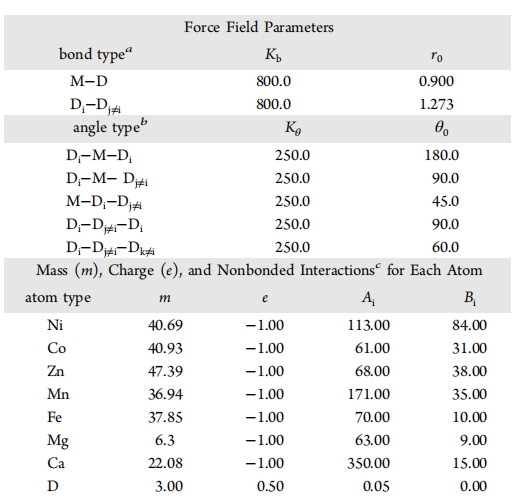
Duarte Model

图7.2 Duarte多点离子模型

因此如果需要在GROMAC中简单可用的多点离子参数，可选择Åqvist和Warshel等人的初版参数作为初猜，在现代模拟算法(如PME)/引擎下进行优化。或者将哑原子的 $\sigma_D$ 和 $\epsilon_D$ 都给出。Zhang等人在研究Ryanodine receptors (RyR)时就使用第二种策略优化了Ca²⁺离子的7个参数。和之前参数拟合中多固定经验参数不同，Zhang等人优化过程对所有参数使用了系统搜索的方法，工作量极大。他们的Ca²⁺离子参数可从Git仓库获取，该参数与AMBER蛋白参数匹配情况仍有待验证。

多点离子模型与单点非键离子模型的优化目标基本一致，溶剂相的HFE，IOD，NC都需要进行匹配。除此之外，多点模型存在的主要意义在于生物大分子的模拟，因此多点模型往往也要考虑与蛋白配位时的构象稳定性和结合自由能。如Zhang等人就优化了多点Ca²⁺离子模型在Ca²⁺离子结合蛋白中的亲和力，Duarte等人优化了多种金属结合蛋白的RMSD等。值得注意的是，Zhang等人在研究Ca²⁺离子多点模型时，发现无法同时满足Ca²⁺离子的溶剂化性质和蛋白结合性质，因此他们巧妙地将离子-水的LJ参数拆出后单独优化，最终获得了与CHARMM36和TIP3P模型匹配的Ca²⁺离子多点模型，且适配GROMACS模拟引擎。

代码2. Zhang等人多点Ca²⁺离子与水的非键参数在GROMACS的ffnonbond.itp中的写法

## ffnonbond
[ atomtypes ]
......
......
  Dz       28.08    0.0000  A       0.267     6.78
  Da       2.0      0.0000  A       0.0095     2.2
......

[ nonbond_params ]
; type1  type2  1  sigma	 epsilon
  Dz    OT  1  .27842871134150000000 1.57541137484785223953
  Dz    HT  1  .14090067622225000000 .86637728502079277447

金属离子模拟要注意力场匹配

旧力场无法适配PME

翻阅AMBER力场中的parm99.dat，可见AMBER99中的离子力场参数：

# parm99.dat
  Li          1.1370  0.0183             Li+ Aqvist JPC 1990,94,8021. (adapted)
  IP          1.8680  0.00277            Na+ Aqvist JPC 1990,94,8021. (adapted)
  Na          1.8680  0.00277            Na+ Aqvist JPC 1990,94,8021. (adapted)
  K           2.6580  0.000328           K+  Aqvist JPC 1990,94,8021. (adapted)
  Rb          2.9560  0.00017            Rb+ Aqvist JPC 1990,94,8021. (adapted)
  Cs          3.3950  0.0000806          Cs+ Aqvist JPC 1990,94,8021. (adapted)
  MG          0.7926  0.8947             Mg2+ Aqvist JPC 1990,94,8021.(adapted)
  C0          1.7131  0.459789           Ca2+ Aqvist JPC 1990,94,8021.(adapted)
  Zn          1.10    0.0125             Zn2+, Merz,PAK, JACS,113,8262,(1991)

早期的离子模型，比如AMBER99中的离子模型，甚至包括后续继承此套参数的AMBER09，AMBER12，AMBER14等，使用的离子模型主要来自Åqvist模型，以及Merz模型。但在Merz等人在现代AMBER11引擎中模拟时，发现Åqvist模型的计算结果与原始论文存在巨大误差。

Table 7.2. Åqvist离子参数在PME下的计算误差

ions	HFE Expt (kcal/mol)	HFE in AMBER Engine	HFE in Åqvist Paper	Merz 2013 TIP3P
Zn²⁺	-467.3	-443.8	NA	-467.4
Mg²⁺	-437.6	-432.6	-455.9 ± 2.6	-437.7
Ca²⁺	-420.7	-307.0	-380.6 ±1.3	-419.9

HFE实验值引自 Marcus, Y. J. Chem. Soc., Faraday Trans. 1991, 87, 2995−2999.

误差产生的原因在于，MD引擎在发展中对长程静电势进行了计算精度和速度的优化，即采用了Particle Mesh Ewald (PME)方法，而Åqvist在1990年时的MD方法还没有PME来计算长程静电势，因此在使用支持PME的AMBER或CHARMM力场时无脑复制Åqvist的离子参数在现在是非常危险的行为，特别是在当研究金属离子本身的特性和金属蛋白相关研究时。这里建议改用Merz团队发表的最新离子力场，这里给出生物体系模拟常用离子的非键模型，同时也建议读者放弃老旧的TIP3P和TIP4P，使用较新的OPC系列或TIPXP-FB系列水模型：

Table 7.3. Merz离子参数

ions	TIP3P^a		OPC3^b		OPC^b		TIP3P-FB^b		TIP4P-FB^b
	$\epsilon$	$\sigma$	$\epsilon$	$\sigma$	$\epsilon$	$\sigma$	$\epsilon$	$\sigma$	$\epsilon$	$\sigma$
Li⁺	\	\	1.270	0.00325650	1.242	0.00216058	1.260	0.00282180	1.240	0.00209587
Na⁺	\	\	1.469	0.03012160	1.467	0.02960343	1.459	0.02759452	1.448	0.02499549
K⁺	\	\	1.703	0.14021803	1.702	0.13953816	1.705	0.14158262	1.685	0.12823270
Ag⁺	\	\	1.335	0.00761745	1.316	0.00602547	1.328	0.00699604	1.313	0.00580060
Mg²⁺	1.360	0.01020237	1.363	0.01055378	1.330	0.0071693	1.363	0.01055378	1.342	0.00828195
Ca²⁺	1.649	0.09788018	1.628	0.09399072	1.608	0.08337961	1.635	0.09788018	1.627	0.09344247
Zn²⁺	1.271	0.00354287	1.280	0.00374505	1.219	0.00150903	1.276	0.00354287	1.234	0.00191142
Cu²⁺	1.218	0.00160860	1.228	0.00174080	1.178	0.0007549	1.223	0.00160860	1.181	0.00089969
Fe²⁺	1.353	0.00952704	1.356	0.00974813	1.323	0.00657749	1.356	0.00974813	1.334	0.00752608
Co²⁺	1.299	0.00523385	1.306	0.00530214	1.263	0.00294683	1.304	0.00516628	1.277	0.00359255
Mn²⁺	1.407	0.01669760	1.410	0.01738340	1.381	0.01286460	1.411	0.01755812	1.394	0.01476261
F^-	\	\	1.818	0.22795460	1.840	0.24650465	1.834	0.24140216	1.845	0.25078000
Cl^-	\	\	2.306	0.64226672	2.360	0.67878870	2.300	0.63803333	2.313	0.64716164
Br^-	\	\	2.501	0.76074098	2.499	0.75971103	2.481	0.75027433	2.454	0.73554824
I^-	\	\	2.780	0.87175814	2.900	0.90300541	2.742	0.86005879	2.804	0.87867445

a. CM parameters compatible with TIP3P arefor JTTC,9,6,2733 (2013)

b. CM parameters for Monovalent ions are from JCIM,61,869−880 (2021), for Divalent metal ions are from JCTC,16,4429 (2020)

单位： $\epsilon(Å)$ ， $\sigma$ (kcal/mol)

AMBER中Zn²⁺共价力场误用

AMBER力场中的Zn²⁺还有一个非常隐蔽的误用： Merz等人在JACS,113,8262,(1991)论文中发表的Zn²⁺参数来自于Ligand-Zn²⁺-(HIS)₃配位蛋白中的成键离子模型，而不是游离的非键离子模型，因此只有在配合成键模型/杂化模型时才可以使用该参数。Merz等人在JTTC,9,6,2733 (2013)，JCTC,10,289, (2014)和JCTC,16,7,4429 (2020)中各发表了一组新的Zn²⁺参数，可用于游离的Zn²⁺模拟。两组参数的r_d有着非常明显的变化，水溶液中的Zn²⁺离子模型的原子半径显著高于配位的Zn²⁺离子模型。这一参数误用也被继承在了GROMACS或其他模拟引擎中的AMBER力场参数中，使用时要格外注意。在GROMACS文件中，可通过在[ nonbonded ]参数块下添加[ nonbond_params ]参数块，指定特定原子间如Zn²⁺与水分子的O和H之间的VDW参数。

金属离子力场参数选择

b. 一般情况：目前的单点非键离子模型对HFE有定向优化，因此除去有特定空间配位要求的情况，单点非键离子模型对能量方面的研究足够优秀；

a. 研究金属-蛋白配合物：如果金属和蛋白之间结构稳定，不需要模拟金属离子的解离/结合过程，则使用MCPB.py或Sobtop进行共价离子模型参数化；如果需要兼顾金属离子的解离/结合研究，或不会使用MCPB.py，可以使用多点离子模型；

b. 研究离子通道的转运、金属离子的结合/解离等可逆过程：使用多点离子模型或单点非键离子模型，如果结合过程中设计离子的配位，则多点离子模型略优于非键单点离子模型。

另外，上世纪80年代发表的TIP3P和TIP4P在过去40年时间后，已经落后于新的水模型，因此最新离子模型都使用较新的水模型如OPC系列，TIPXP-EW或TIXP-FB系列等进行拟合，因此建议读者直接将自己的力场参数的水模型和离子模型直接替换到现代力场模型，在计算量完全不变的情况下有着更准确的计算结果。

PS: 感兴趣的读者可进一步阅读Li和Merz等人2017年发表的Chemical Review文章《Metal Ion Modeling Using Classical Mechanics》。

参考文献

[1] Li, P. , & Merz, K. M. . (2017). Metal ion modeling using classical mechanics. Chemical Reviews, 117(3), 1564-1686.

[2] Zhang, A. , Yu, H. , Liu, C. , & Song, C. . (2020). The Ca2+ permeation mechanism of the ryanodine receptor revealed by a multi-site ion model. Nature Communications, 11(1).

[3] Chakravorty, D. K., Wang, B., Ucisik, M. N., & Merz Jr, K. M. (2011). Insight into the cation−π interaction at the metal binding site of the copper metallochaperone CusF. Journal of the American Chemical Society, 133(48), 19330-19333.

[4] Li, P. , & Merz, K. M. . (2016). Mcpb.py: a python based metal center parameter builder. Journal of Chemical Information and Modeling, 599.

[5] Sakharov, D. V. , & Lim, C. . (2005). Zn protein simulations including charge transfer and local polarization effects. Journal of the American Chemical Society, 127(13), 4921-4929.

[6] Stuart, S. J.; Berne, B. Effects of Polarizability on the Hydration of the Chloride Ion. J. Phys. Chem. 1996, 100, 11934−11943.

[7] Åqvist, J., & Warshel, A. (1990). Free energy relationships in metalloenzyme-catalyzed reactions. Calculations of the effects of metal ion substitutions in staphylococcal nuclease. Journal of the American Chemical Society, 112(8), 2860-2868.

[8] Li, P., Roberts, B. P., Chakravorty, D. K., & Merz Jr, K. M. (2013). Rational design of particle mesh Ewald compatible Lennard-Jones parameters for+ 2 metal cations in explicit solvent. Journal of chemical theory and computation, 9(6), 2733-2748.

[9] Sengupta, A. , Li, Z. , Song, L. F. , Li, P. , & Merz, K. M. . (2021). Parameterization of monovalent ions for the OPC3, OPC, TIP3P-FB, and TIP4P-FB water models (vol 61, pg 869, 2021). Journal of chemical information and modeling(7), 61.

[10] Li, Z., Song, L. F., Li, P., & Merz Jr, K. M. (2020). Systematic parametrization of divalent metal ions for the OPC3, OPC, TIP3P-FB, and TIP4P-FB water models. Journal of chemical theory and computation, 16(7), 4429-4442.

[11] Hoops, S. C. , Anderson, K. W. , & Merz, K. M. . (1991). Force field design for metalloproteins. Journal of the American Chemical Society, 113(22), 8262-8270.

[12] Saxena, A. , & Sept, D. . (2013). Multisite ion models that improve coordination and free energy calculations in molecular dynamics simulations. Journal of Chemical Theory & Computation, 9(8), 3538-3542.

[13] Duarte, F. , Bauer, P. , Barrozo, A. , Amrein, B. A. , Purg, M. , & Åqvist, Johan, et al. (2014). Force field independent metal parameters using a nonbonded dummy model. Journal of Physical Chemistry B, 118(16), 4351-4362.

[14] Oelschlaeger, P. , Klahn, M. , Beard, W. A. , Wilson, S. H. , & Warshel, A. . (2007). Magnesium-cationic dummy atom molecules enhance representation of dna polymerase β in molecular dynamics simulations: improved accuracy in studies of structural features and mutational effects. Journal of Molecular Biology, 366(2), 687-701.

[15] Marcus, Y. . (1993). Thermodynamics of solvation of ions. part 6.—the standard partial molar volumes of aqueous ions at 298.15 k. Journal of the Chemical Society, Faraday Transactions, 89(4), 713-718.