定制小分子力场(六)：GAFF力场的参数拟合-软参数

前一篇文章中讨论了键长键角的硬参数拟合，本文继续讨论力场参数拟合中的软参数拟合。软参数意义重大，软参数对分子间的相互作用和分子构象影响最大，硬参数影响较小，因此一般都先拟合软参数，再拟合硬参数。本章将对软参数的拟合方法进行简述，对软参数中的二面角参数进行详解。

软参数拟合

库仑参数拟合

库仑参数拟合可阅读本教程第四章。拟合静电势电荷，或对静电势复现好的电荷，最适合基于力场的分子模拟。因为在分子力场中，分子和分子之间的静电相互作用，是各分子内原子之间的使用库仑势函数定义静电相互作用。因此能够通过库仑势函数对分子表面静电势进行复现的电荷模型能够更好地模拟分子间的相互作用。RESP电荷和AM1-BCC是GAFF力场下的最适电荷。

范德华参数拟合

扫描原子间随着距离变化产生的势能面，然后用范德华作用能表达式拟合这个势能面，即不断改变势阱参数和半径参数，直到两势能面差距的平方和最小，即可得到范德华作用参数。

遗憾的是，这样得到的参数，并不能用于分子模拟。因为势能面一般是在气相中优化得到的，缺少多体效应。在凝聚态中，由于诱导，极化等效应，体现为介电常数不同，故而其势能面与在气相中有很大差别。电荷也不同，自然范德华参数也就难以精确获取。

我们目前主要使用用的范德华参数从是Dr.William Jorgensen（OPLS力场开发者）用以下方法得到的：选定初始参数，做分子模拟，然后看模拟结果和实验值的差别，然后调整参数，继续模拟，直到达到收敛标准。这是一个约束数量少于未知数的线性方程组，是一个多解问题。所以要加上很多经验修正。特别是需要先固定一些参数，如C, H的电荷和范德华参数。并根据化学性质区分不同的原子类型，然后给不同的原子类型以不同的参数。也有学者如Dr. David Mobley通过计算溶剂化能优化GAFF力场的范德华参数。也因为范德华参数优化如此困难，所以如AMBER，GAFF和MMFF94力场等，大量借用了OPLS力场的范德华参数。

也有力场如全周期力场UFF通过解量化波函数的交叉量来计算吸引项，通过FKS的Hartree-Fock量的上界计算排斥项。这样的力场在模拟凝聚相时可想而知存在极大误差，但是如果GAFF力场中缺失某些元素的范德华参数，可先查找OPLS力场参数，再在UFF力场中寻找对应参数进行模拟。

二面角参数

二面角参数是力场参数中最明显的短板，有缺陷的二面角参数会甚至导致分子构象发生不和常理的翻转。比如乙酰基噻吩分子的GAFF力场下，乙酰基平面与噻吩环平面呈30°角时能量最低，但量化扫描的结果是乙酰基平面与噻吩环平面呈0°时能量最低，且O和S同侧时能量低于O和C同侧。再比如联噻吩结构，两个噻吩环在GAFF力场下虽然最低能量构象和量化一致为0°，但是GAFF力场的势垒超过~50 kcal/mol，在常规动力学下无法翻转，但实际上量化扫描的二面角势垒只有~5 kcal/mol，常规动力学模拟下应该可以发生自由旋转。因此在GAFF力场中，对非常见体系的二面角参数应当进行提前的检查。

二面角拟合步骤

二面角参数的拟合可以简单分为5步：

1. 将二面角涉及的片段截取出以减少分子内非键相互作用干扰和计算量
2. 使用量化软件对片段的二面角进行柔性或刚性扫描，获得势能面和构象
3. 使用gmx mdrun -rerun命令在关闭二面角参数(另势垒为0)的分子力场对第2步获得的扫描构象进行能量计算，获得1,4相互作用能和柔性扫描中变化参数带来其他作用能的势能面
4. 使用量化势能面减去第3步获得的势能面，获得二面角势能面
5. 使用周期函数拟合第4步计算获得的二面角势能面，获得二面角参数(势垒，相位，周期)

第1步拆分时，至少要保证二面角再往外延伸一个原子的片段与实际分子相同；如果二面角的一部分在环上，则将第1个环完整包含在小分子里，尽量去掉不必要的取代。

第2步使用柔性扫描最理想，如果计算条件不允许，可以刚性扫描后对极值点进行限制二面角的优化。

第3-4步，有时扫描出的1,4相互作用能很不平滑，这是因为柔性扫描导致键长键角变化后引起的1,4相互作用能波动，必要时可以在这一步换用刚性扫描构象计算1,4相互作用能。有时1,4相互作用能差异远大于二面角差异时，可以考虑在最终力场里删除该1,4相互作用能对，完全通过周期函数同时模拟二面角势能和1,4相互作用。

第5步拟合时可以用多个周期函数，周期函数数量越多拟合越准确，力场复杂度越高，一般1-2两个足够，3-4个偏多，4个以上有可能是过拟合了量化扫描不稳定导致的能量振荡。

最后，如果势能面过于复杂，也不需要追求百分百地拟合，尽量将能垒和最低能量构象拟合，甚至必要时只要保证最低能量构象正确即可。

二面角参数组合

以下是几种常用的周期和相位组合，对于大多数情况，使用以下参数组合就可以描述几乎所有的二面角势能面。

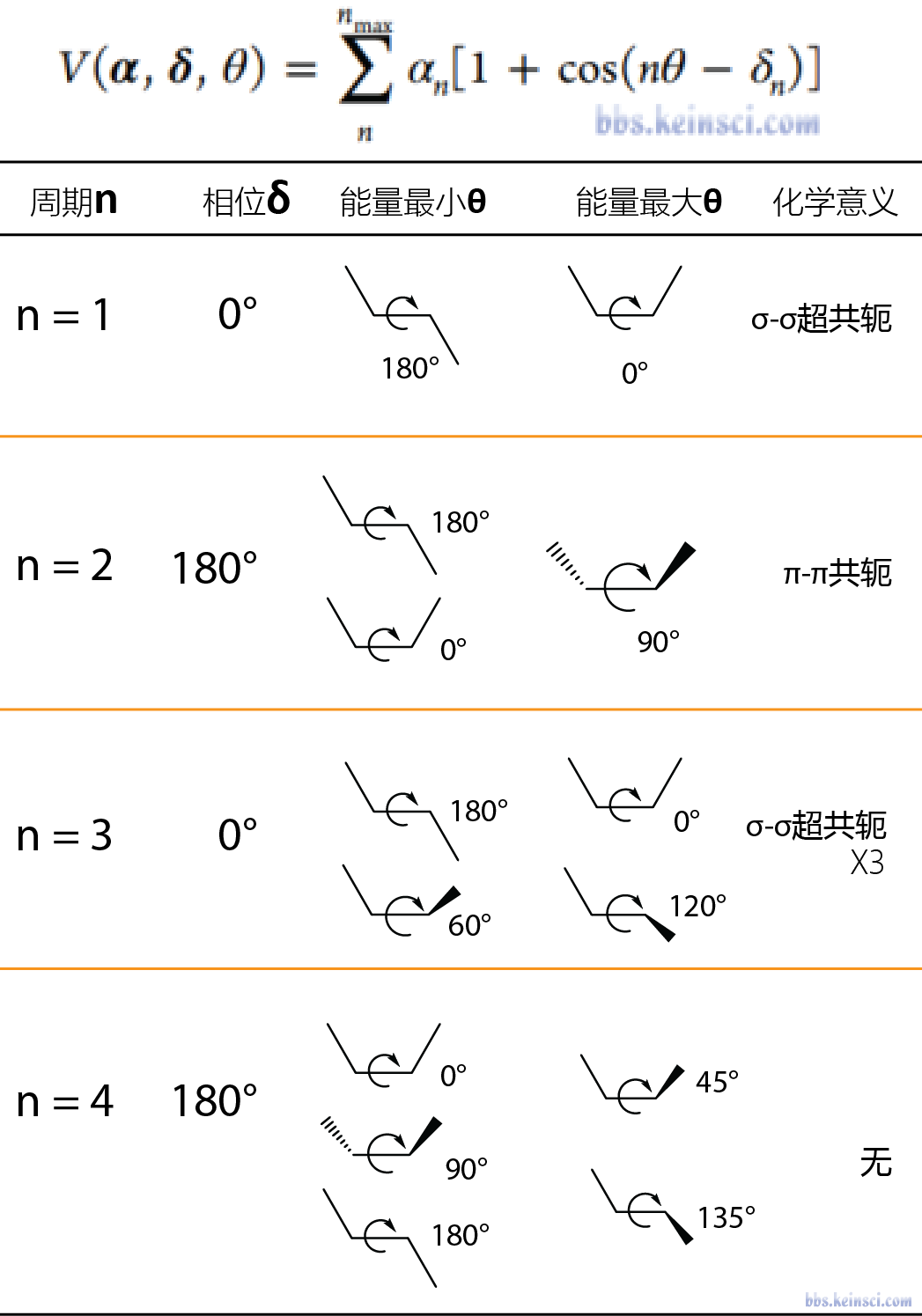
这里引用科音论坛中的二面角相位周期速查表进行理解：

• n=1时相位为0，这时二面角处于反式共平面能量最低，而顺式共平面能量最高。由于这里假设排除了1,4非键作用，这种势能面可以看出是σ-σ超共轭效应的结果，如乙烯的二面角。如果将相位改为180，则对应顺式能量最低构象，如N甲基甲酰胺。
• n=2时相位为180，这时二面角共面能量最低，而垂直时能量最高，对应于π-π共轭效应，如联苯的二面角。如果将相位改为0，则垂直时能量最低，如乙苯的苄基和甲基间的二面角垂直时能量最低。
• n=3时相位为0，这时二面角在60 180 300 能量最低，而在0 120 240能量最高，可以对应于经典的乙烷的构象，前者是交叉式，后者是重叠式，这里可以看成是3个超共轭共同作用的结果。
• n=4时相位为180，这时二面角在0 90 180能量最低，而在45 135能量最高，化学中少有这样的作用，主要作为补充复杂二面角势能面的拟合曲线存在。

通过以上经验规则，在拟合二面角时可以只通过拟合力常数(正数)来完成二面角的拟合。

二面角参数拟合Python实现

通过对cosine函数进行积化和差后，可以使用最小二乘法可以对第4步获得的二面角势能面进行拟合。我们为了便于操作，使用scipy包提供的least_squares函数进行最小二乘法求解。scipy使用Levenberg-Marquardt算法进行最小二乘法求解，这是一种迭代方法，因此least_squares函数需要初猜参数，与纯数学解析法略有差异。

首先导入依赖包

import numpy as np
from scipy import linalg
from scipy.optimize import least_squares
import matplotlib.pyplot as plt

我们假设一套参数组合 (4.2, 1, 180°)，(4.2, 2, 180°)：

def dihedral(x, p):
    k,n,t = p
    return k * (1 + np.cos( n * x - t))

x = np.linspace(-np.pi, np.pi, 360)
y0 = dihedral(x, (4.2, 2, np.pi)) + dihedral(x, (4.2, 1, np.pi)) + dihedral(x, (2, 1, np.pi))
y1 = y0 + 0.5*np.random.randn(len(x))

plt.scatter(x, y1)

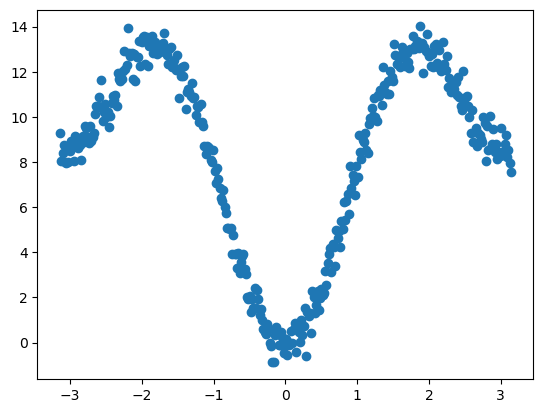
使用最小二乘法拟合可以获得二面角参数：

params = [(1,0), (1, np.pi), (2,0), (2, np.pi), (3,0), (3, np.pi)]

min_cost = 1e9
min_id = None
min_p = None



func = lambda a, x:  a * (1 + np.cos( param[0] * x - param[1]))
for i, parami in enumerate(params):
    for _j, paramj in enumerate(params[i:]):
        j = i + _j
        func = lambda a, y, x: y - a[0] * (1 + np.cos( parami[0] * x - parami[1])) - a[1] * (1 + np.cos( paramj[0] * x - paramj[1]))

        plsq = least_squares(func, (1, 1), args=(y1, x))
        # print((i, j), round(plsq.x[0],2), round(plsq.x[1],2), round(plsq.cost,2))
        if plsq.cost < min_cost:
            min_cost = plsq.cost
            min_id = i, j
            min_p = plsq.x

if abs(min_p[0]) < 0.2:
    if min_id[0] == min_id[1]:
        min_p[1] += min_p[0]
    else:
        paramj = params[min_id[1]]
        func = lambda a, y, x: y - a * (1 + np.cos( paramj[0] * x - paramj[1]))
        plsq = least_squares(func, min_p[1], args=(y1, x))
        min_p[1] = plsq.x
    min_p[0] = 0
elif abs(min_p[1]) < 0.2:
    if min_id[0] == min_id[1]:
        min_p[0] += min_p[1]
    else:
        parami = params[min_id[0]]
        func = lambda a, y, x: y - a * (1 + np.cos( parami[0] * x - parami[1]))
        plsq = least_squares(func, min_p[0], args=(y1, x))
        min_p[0] = plsq.x
    min_p[1] = 0
    
parami = params[min_id[0]]
paramj = params[min_id[1]]
# print(min_id)
print(round(min_p[0],2), parami, round(min_p[1],2), paramj)
func = lambda a, x:  a[0] * (1 + np.cos( parami[0] * x - parami[1])) + a[1] * (1 + np.cos( paramj[0] * x - paramj[1]))

plt.scatter(x[10:-10], y1[10:-10])
plt.scatter(x, func(min_p, x))
plt.plot()

[out]:  4.21 (1, 3.141592653589793) 4.16 (2, 3.141592653589793)

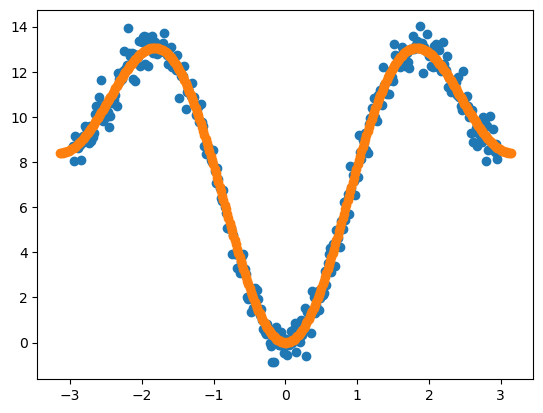
拟合获得二面角参数组合(4.21, 1, 180°)，(4.16, 2, 180°)，与我们未添加噪声的二面角参数基本一致。

对于更复杂的二面角：

x = np.linspace(-np.pi, np.pi, 360)
y0 = dihedral(x, (1.2, 4, np.pi)) + dihedral(x, (2.2, 2, 0))
y1 = y0 + 0.1*np.random.randn(len(x))

plt.scatter(x, y1)

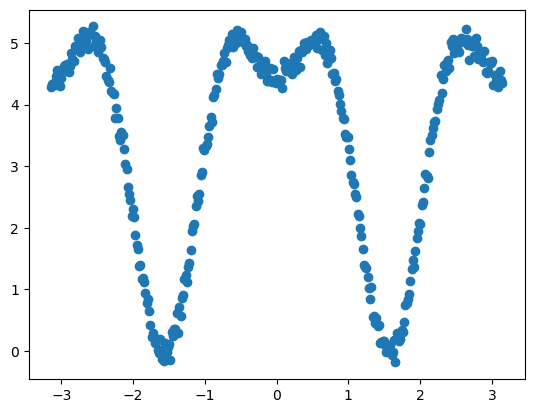
需要引入周期为4的二面角参数：

params = [(1,0), (1, np.pi), (1, np.pi/2), (2,0), (2, np.pi), (2, np.pi/2), (3,0), (3, np.pi), (3, np.pi/2), (4,0), (4, np.pi), (4, np.pi/2)]

min_cost = 1e9
min_id = None
min_p = None



func = lambda a, x:  a * (1 + np.cos( param[0] * x - param[1]))
for i, parami in enumerate(params):
    for _j, paramj in enumerate(params[i:]):
        j = i + _j
        func = lambda a, y, x: y - a[0] * (1 + np.cos( parami[0] * x - parami[1])) - a[1] * (1 + np.cos( paramj[0] * x - paramj[1]))

        plsq = least_squares(func, (1, 1), args=(y1, x))
        # print((i, j), round(plsq.x[0],2), round(plsq.x[1],2), round(plsq.cost,2))
        if plsq.cost < min_cost:
            min_cost = plsq.cost
            min_id = i, j
            min_p = plsq.x

if abs(min_p[0]) < 0.2:
    if min_id[0] == min_id[1]:
        min_p[1] += min_p[0]
    else:
        paramj = params[min_id[1]]
        func = lambda a, y, x: y - a * (1 + np.cos( paramj[0] * x - paramj[1]))
        plsq = least_squares(func, min_p[1], args=(y1, x))
        min_p[1] = plsq.x
    min_p[0] = 0
elif abs(min_p[1]) < 0.2:
    if min_id[0] == min_id[1]:
        min_p[0] += min_p[1]
    else:
        parami = params[min_id[0]]
        func = lambda a, y, x: y - a * (1 + np.cos( parami[0] * x - parami[1]))
        plsq = least_squares(func, min_p[0], args=(y1, x))
        min_p[0] = plsq.x
    min_p[1] = 0
    
parami = params[min_id[0]]
paramj = params[min_id[1]]
print(min_id)
print(round(min_p[0],2), parami, round(min_p[1],2), paramj)
func = lambda a, x:  a[0] * (1 + np.cos( parami[0] * x - parami[1])) + a[1] * (1 + np.cos( paramj[0] * x - paramj[1]))

plt.scatter(x[10:-10], y1[10:-10])
plt.scatter(x, func(min_p, x))
plt.plot()

[out]:  2.2 (2, 0) 1.2 (4, 3.141592653589793)

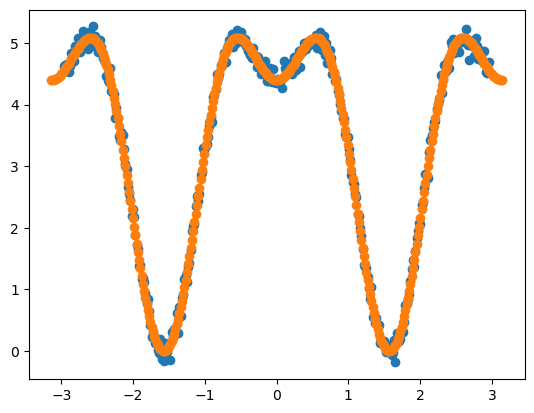
拟合获得二面角参数组合(2.2, 2, 0°)，(1.2, 4, 180°)。

小结

本章对软参数的拟合进行了介绍：库仑参数在第四章进行了详述，范德华参数难以拟合，一般不建议自行拟合，二面角参数则可通过拟合提升分子力场精度。本章对二面角参数的拟合方法进行了较为详细的描述，并且对二面角参数的拟合进行了代码实现。