定制小分子力场(五)：GAFF力场的参数拟合-硬参数

Posted on

前文提到了分子力场中的电荷模型的类型和历史沿革，接下来我们将讨论分子力场中的剩余部分的参数来源。除针对库仑势的电荷模型外，本文将讨论库仑势参数，键长，键角和二面角参数的拟合。力场的拟合可以大致分为硬参数拟合和软参数拟合，硬参数包含键长和键角参数，软参数包含范德华参数，库仑参数(电荷模型)和二面角参数。软参数对分子间的相互作用和分子构象影响最大，硬参数影响较小，因此一般都先拟合软参数，再拟合硬参数。即可按照库仑参数，范德华参数，二面角参数，键长和键角参数顺序拟合。本文以从简到难的顺序，先讨论键长和键角的拟合方法。

硬参数拟合

GAFF的硬参数拟合

GAFF力场平衡键长参数来源主要有4个：1. J. Chem. Soc., Perkin Trans. 2, 1987, S1-S19中的X射线晶体衍射结构，2. J.Phys Chem Ref Data., 8, 1979, 619-722中的X射线晶体衍射结构，3. MP2/6-31G*级别优化结构，4. B3LYP/6-31G*级别优化结构。

力常数参数来源主要有3个：1. 实验测定的波数vv，经过波数公式可以计算得到的力常数；2. MP2/6-311G+(d,p)级别量化计算得到的振动频率乘缩放系数0.9496后计算的力常数；3. 根据前两种高精度放法计算的力场数，使用Badger规则和线性回归拟合的其他键的力常数。

前两种来源比较直观，第三种来源类似于MAFF94力场，即使用高精度的力场参数补全未知的力场参数。比如对键角来说，Θ(A−B−C)\Theta_{(A-B-C)}的键角大小可以通过Θ(A−B−A)\Theta_{(A-B-A)}和Θ(C−B−C)\Theta_{(C-B-C)}的平均得到，力常数则使用经验公式根据(A-B-C)原子类型拟合。

尽管使用高精度的力场参数补全未知的键长键角力场参数，极大节省了计算量，但是这种组合办法仍然是有风险的，特别是对键角的影响。举例来讲，对于6并6的芳香体系，每个重原子X-X-X键角都是120°，而对于5并5的芳香体系，每个重原子X-X-X键角应该接近108°，但是GAFF的组合方法可能仍会给5并5体系的X-X-X键角120°的平衡角度，最终结果会导致5并5芳香体系的平面发生折叠。

定制化硬参数拟合

对于特定的小分子，也有简单通用的方法在量化计算结果上实现对力场参数的拟合。使用HF/6-31G*或更高级别的量化方法优化分子构型，我们可以获得分子低能构象下的键长和键角的平衡距离；同时计算振动频率，即可根据振动频率计算键长或键角的力场数。但是对于复杂分子，振动频率往往是多维且复杂的，因此我们使用振动分析过程中的Hessian矩阵进行振动分解。

键长参数

Fig. 5.1

对于EE的所有二阶导可得FF的Hessian矩阵：

F=[∂2E∂2x1∂2x1∂2E∂2x1∂2y1∂2E∂2x1∂2z1⋯∂2E∂2x1∂2zn∂2E∂2y1∂2x1∂2E∂2y1∂2y1∂2E∂2y1∂2z1⋯∂2E∂2y1∂2zn⋮⋮⋮⋱⋮∂2E∂2zn∂2x1∂2E∂2zn∂2y1∂2E∂2zn∂2z1⋯∂2E∂2zn∂2zn](5.1)F = \begin{bmatrix} \frac{\partial ^2 E}{\partial ^2 x_1 \partial ^2 x_1} & \frac{\partial ^2 E}{\partial ^2 x_1 \partial ^2 y_1} & \frac{\partial ^2 E}{\partial ^2 x_1 \partial ^2 z_1} & \cdots & \frac{\partial ^2 E}{\partial ^2 x_1 \partial ^2 z_n} \\\\ \frac{\partial ^2 E}{\partial ^2 y_1 \partial ^2 x_1} & \frac{\partial ^2 E}{\partial ^2 y_1 \partial ^2 y_1} & \frac{\partial ^2 E}{\partial ^2 y_1 \partial ^2 z_1} & \cdots & \frac{\partial ^2 E}{\partial ^2 y_1 \partial ^2 z_n} \\\\ \vdots & \vdots & \vdots & \ddots & \vdots \\\\ \frac{\partial ^2 E}{\partial ^2 z_n \partial ^2 x_1} & \frac{\partial ^2 E}{\partial ^2 z_n \partial ^2 y_1} & \frac{\partial ^2 E}{\partial ^2 z_n \partial ^2 z_1} & \cdots & \frac{\partial ^2 E}{\partial ^2 z_n \partial ^2 z_n} \\\\ \end{bmatrix} \tag{5.1}

取原子A，B的坐标分量的Hessian矩阵部分：

[FAB]=−[∂2E∂2xA∂2xB∂2E∂2xA∂2yB∂2E∂2xA∂2zB∂2E∂2yA∂2xB∂2E∂2yA∂2yB∂2E∂2yA∂2zB∂2E∂2zA∂2xB∂2E∂2zA∂2yB∂2E∂2zA∂2zB]×[∂rAB](5.2)[F_{AB}] = - \begin{bmatrix} \frac{\partial ^2 E}{\partial ^2 x_A \partial ^2 x_B} & \frac{\partial ^2 E}{\partial ^2 x_A \partial ^2 y_B} & \frac{\partial ^2 E}{\partial ^2 x_A \partial ^2 z_B} \\\\ \frac{\partial ^2 E}{\partial ^2 y_A \partial ^2 x_B} & \frac{\partial ^2 E}{\partial ^2 y_A \partial ^2 y_B} & \frac{\partial ^2 E}{\partial ^2 y_A \partial ^2 z_B} \\\\ \frac{\partial ^2 E}{\partial ^2 z_A \partial ^2 x_B} & \frac{\partial ^2 E}{\partial ^2 z_A \partial ^2 y_B} & \frac{\partial ^2 E}{\partial ^2 z_A \partial ^2 z_B} \\\\ \end{bmatrix} \times [\partial r_{AB}] \tag{5.2}

因此[kAB][k_{AB}]即为：

[kAB]=−[∂2E∂2xA∂2xB∂2E∂2xA∂2yB∂2E∂2xA∂2zB∂2E∂2yA∂2xB∂2E∂2yA∂2yB∂2E∂2yA∂2zB∂2E∂2zA∂2xB∂2E∂2zA∂2yB∂2E∂2zA∂2zB](5.3)[k_{AB}] = - \begin{bmatrix} \frac{\partial ^2 E}{\partial ^2 x_A \partial ^2 x_B} & \frac{\partial ^2 E}{\partial ^2 x_A \partial ^2 y_B} & \frac{\partial ^2 E}{\partial ^2 x_A \partial ^2 z_B} \\\\ \frac{\partial ^2 E}{\partial ^2 y_A \partial ^2 x_B} & \frac{\partial ^2 E}{\partial ^2 y_A \partial ^2 y_B} & \frac{\partial ^2 E}{\partial ^2 y_A \partial ^2 z_B} \\\\ \frac{\partial ^2 E}{\partial ^2 z_A \partial ^2 x_B} & \frac{\partial ^2 E}{\partial ^2 z_A \partial ^2 y_B} & \frac{\partial ^2 E}{\partial ^2 z_A \partial ^2 z_B} \\\\ \end{bmatrix} \tag{5.3}

对矩阵kABk_{AB}进行矩阵分解，可得3个特征值λiAB\lambda_i^{AB}以及对应的特征向量viABv_i^{AB}，λiAB\lambda_i^{AB}就是viABv_i^{AB}方向上的A-B键力常数分量。因此我们计算3个方向的力场数在A-B键方向u^AB\hat{u}^{AB}的投影即可得A-B键力常数krk_r：

kr=∑i=13λiAB∣u^AB⋅v^iAB∣(5.4)k_r = \sum_{i=1}^3 \lambda_i^{AB}|\hat{u}^{AB} \cdot \hat{v}_i^{AB}| \tag{5.4}

键角参数

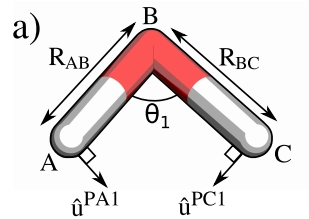
键角参数kΘk_\Theta稍复杂些，对于键角A-B-C，涉及A-B和-CB两个键。

首先定义单位向量uNu_N垂直于平面ABC：

u^N=uAB^×uBC^∣uAB^×uBC^∣(5.5)\hat{u}_N = \frac{\hat{u_{AB}} \times \hat{u_{BC}}}{|\hat{u_{AB}} \times \hat{u_{BC}}|} \tag{5.5}

借助单位向量uNu_N可获得在ABC平面上垂直于AB和垂直于BC的指向键角收缩方向的向量u^PA\hat{u}^{PA}和u^PA\hat{u}^{PA}：

u^PA=u^N×u^ABu^PC=u^CB×u^N(5.6)\hat{u}^{PA} = \hat{u}_{N} \times \hat{u}_{AB} \\\\ \hat{u}^{PC} = \hat{u}_{CB} \times \hat{u}_{N} \tag{5.6}

然后我们将AB和CB的特征向量投影到键角收缩方向：

kPA=∑i=13λiAB∣u^PA⋅v^iAB∣kPC=∑i=13λiCB∣u^PC⋅v^iCB∣(5.7)k_{PA} = \sum_{i=1}^3 \lambda_i^{AB}|\hat{u}^{PA} \cdot \hat{v}_i^{AB}| \\\\ k_{PC} = \sum_{i=1}^3 \lambda_i^{CB}|\hat{u}^{PC} \cdot \hat{v}_i^{CB}| \tag{5.7}

类似两个顺序链接的弹簧，键角的力场数kΘk_\Theta与kPAk_{PA}和kPCk_{PC}的关系近似为：

1kΘ=1RAB2kPA+1RBC2kPA(5.8)\frac{1}{k_\Theta} = \frac{1}{R_{AB}^2 k_{PA}} + \frac{1}{R_{BC}^2 k_{PA}} \tag{5.8}

则可获取键角的力场数kΘk_\Theta。

改进的Seminario方法mSeminario

Seminario方法对键角的力场数评估的前提假设是能量变化与原子A沿着u^PA\hat{u}^{PA}变化时，仅影响A-B-C键角。但实际上在复杂体系中，ABC的键角变化时，会影响它的补角的变化。比如我们考虑氯苯的三个二面角，C.A-C.B-C.C，C.A-C.B-Cl.D，C.C-C.B-Cl.D，当C.A-C.B-C.C键角变化时，C.A-C.B-Cl.D和C.C-C.B-Cl.D都会同时变化。因此使用Seminario方法对键角的力场数评估会导致这一个键角的力参数会包含另两个键角的力常数成分，导致键角参数的高估。

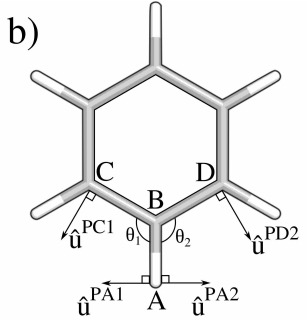
Fig. 5.2

将ABC键角的A原子向ABC键角收缩方向设为u^PA1\hat {u}_{PA1}向量，将ABD键角的A原子向ABD键角收缩方向设为u^PA2\hat {u}_{PA2}向量，则Seminario方法的键角力常数可改写为：

kPA1Seminario=kPA1(Δx)2+kPA2(Δx)2=>kPA1Seminario=kPA1(Δx)2+kPA2(Δx∣u^PA1⋅u^PA2∣2)(5.9)k_{PA1}^{Seminario} = k_{PA1}(\Delta x)^2 + k_{PA2}(\Delta x)^2 \\\\ => \\\\ k_{PA1}^{Seminario} = k_{PA1}(\Delta x)^2 + k_{PA2}(\Delta x|\hat{u}_{PA1}\cdot\hat{u}_{PA2}|^2) \tag{5.9}

如苯环的键角ABC键角和ABD键角在同一平面，则可进一步假设kPA1≈kPA1k_{PA1} \approx k_{PA1}，因此Sminario方法下苯环键角力常数被高估两倍。

对于非同一平面的二面角，我们有：

kPA1=kPA1Seminario1+∣u^PA1⋅u^PA2∣2(5.10)k_{PA1} = \frac{k_{PA1}^{Seminario}}{1+|\hat{u}_{PA1}\cdot\hat{u}_{PA2}|^2} \tag{5.10}

因此推广后的Modified Seminario (mSeminario)方法二面角计算公式为：

1kΘ=1+∑i=1N∣u^PA1⋅u^PAi∣−1N−1RAB2kPASeminario+1+∑i=1M∣u^PC1⋅u^PCi∣−1M−1RCB2kPA(5.11)\frac{1}{k_\Theta} = \frac{1+\frac{\sum_{i=1}^N |\hat{u}_{PA1}\cdot\hat{u}_{PAi}|-1}{N-1}}{R_{AB}^2 k_{PA^{Seminario}}} + \frac{1+\frac{\sum_{i=1}^M |\hat{u}_{PC1}\cdot\hat{u}_{PCi}|-1}{M-1}}{R_{CB}^2 k_{PA}} \tag{5.11}

如果N=1 (M=1)N=1 \, (M=1)，则左半部分(右半部分)公式替换为原版的Semiario公式。

二面角和异二面角

从键角的3原子关系可以显而易见地推广到二面角或异二面角参数。对于异二面角，本质是原子偏离平面的能量偏差，因此可以通过将特征值投影在偏离方向获取异二面角的间歇势的力场数。

但是二面角不同，二面角的旋转是周期性的，所以固定角度的Hessian矩阵的特征值仅仅代表此时构象的二面角的力常数。同时，Hessian矩阵是包含所有原子间的相互作用，比如1,4相互作用，因此即便使用Seminario方法获取二面角参数，也要在模拟中关闭对应的1,4相互作用。这些原因导致了单一构象时Seminario方法完全无法拟合二面角参数

Seminario方法的表现

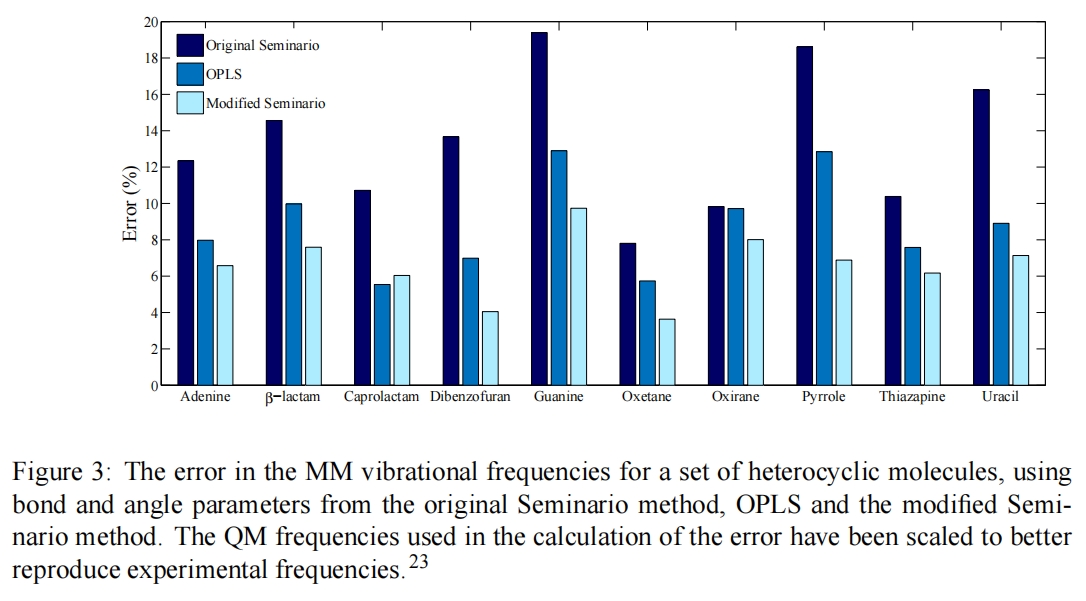
Fig. 5.3

Seminario和mSeminario方法在杂环数据集上对键长键角参数拟合后的分子振动频率的误差表现如图，其中mSeminario方法已经可以超越通用小分子力场OPLS。

Seminario方法代码实现与其他力常数拟合方法

Seminario方法通过量化计算的Hessian矩阵直接获取键长键角的力常数。Seminario方法或mSeminario方法的Python代码实现可参考Github仓库。实际应用可使用Dr.Tian Lu的Sobtop程序。Sobtop支持Gaussian，ORCA和gfn-xtb软件输出的Hessian矩阵文件，可实现Seminario方法和mSeminario方法，甚至可拟合二面角参数。

除Seminario方法外，也有其他使用量化计算的Hessian矩阵获取力常数的方法，如Dr.Ruixing Wang和Dr.Hajime Hirao提出的，以最小化分子力场的Hessian矩阵的和量化Hessian矩阵的差的思想（min∑(HessijQM−HessijMM)2min \sum (Hess_{ij}^{QM}-Hess_{ij}^{MM})^2）的PHF，HHF和IHF方法。同一课题组也针对非共价键或有着强分子内静电作用的键长键角作用提出了Katachi修正法，即迭代地修改平衡常数和力常数，直到分子力场优化的结构表现与量化计算结果一致的平衡距离和Hessian矩阵。Parmhess程序可自动计算HF，HHF和IHF方法，以及了Katachi修正。

小结

本文对力场参数的拟合大致分类为包含二面角，范德华和库仑参数的软参数，以及包含键长，键角，异二面角参数的硬参数。本文针对硬参数拟合，详细介绍了计算简单，应用广泛的Seminario方法和mSeminario方法。也简单提及了一些较新的拟合思想，如PHF，HHF和IHF方法和Katach修正法。PHF，HHF和IHF方法产生的参数对于振动频率的复现情况优于Seminario方法，且两类方法都优于GAFF和OPLS力场参数。读者可以通过Sobtop和Parmhess程序自行计算键长键角参数，更新到GAFF力场小分子拓扑文件中。