定制小分子力场(四)：力场的电荷模型

AMBER力场的御用电荷模型是限制性静电势电荷，Restrained Electro Static Potential (RESP)电荷。对于RESP电荷的思想来源推荐阅读以下两篇Sobereva的博文《RESP拟合静电势电荷的原理以及在Multiwfn中的计算》，以及《RESP2原子电荷的思想以及在Multiwfn中的计算》。针对GAFF小分子力场，Amber团队仍然首推RESP电荷，但是因为RESP电荷需要HF或B3LYP级别的量化计算，因此GAFF同时也提供一种快速的带键校正的半经验电荷模型AM1-BCC。关于各类电荷模型可阅读论文卢天,陈飞武等.原子电荷计算方法的对比[J].物理化学学报,2012(01):1-18.进行大致了解学习。本文将在以上文章基础上对RESP电荷模型和AM1-BCC电荷模型进行一定的补充讲解。

图4.1 不同电荷模型的原子电荷

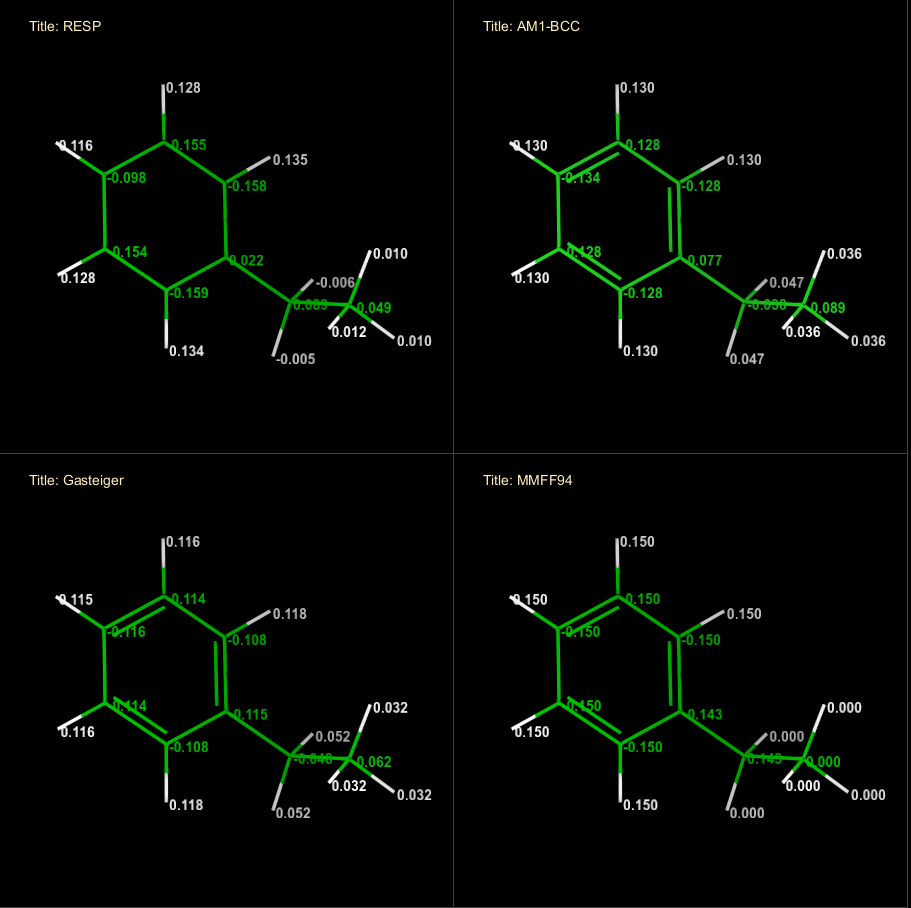
拟合静电势电荷是分子模拟的最佳电荷

拟合静电势电荷，或对静电势复现好的电荷，对于基于力场的分子模拟意义重大。因为在分子力场中，分子和分子之间的静电相互作用，是各分子内原子之间的静电相互作用，使用库仑势函数定义。因此能够对分子表面静电势进行复现的电荷模型能够更好地模拟分子间的相互作用。

基于量化方法拟合静电势电荷通过使原子电荷能尽可能好地重现基于波函数计算的分子范德华表面附近和外侧的静电势来得到，此类电荷也可被称为静电势表面(Electro Static Potential, ESP)电荷。其中最常用的电荷模型包括Merz-Kollman (MK)和CHELPG，两种电荷都是对基于波函数计算的表面静电势格点处电荷值进行最小二乘法拟合获得，两者仅仅是取值点不同。

在静电势电荷基础上，延伸出各类限制性静电势电荷。如RESP电荷则是在此类电荷基础上，通过对轻重原子和对称原子添加限制项，进行修正后的电荷模型。RESP电荷也是AMBER和GAFF力场的御用电荷。电荷模型(CM)系列电荷，如CM1，CM2，CM3，CM4，CM5等，都是对低级别方法下的Mulliken或Löwdin电荷进行键较正的方法，校正参数取决于键两端的原子的元素。与RESP电荷以静电势为主要拟合目的不同，CM电荷最初以偶极矩作为拟合目标。CM电荷是OPLS力场的御用电荷，不过OPLS力场使用CM电荷时会引入缩放系数或额外键校正，如1.14*CM1A-LBCC或1.20*CM5。CHARMM力场下的小分子力场CGenFF电荷模型与也使用MP2/6–31G(d)级别计算的MK电荷进行校正获得，通过一定的高估气相下的分子偶极，来增强凝聚相/水相的模拟表现。

也有使用较低精度的量化模型或完全通过经验参数构建的力场电荷模型。如AM1-BCC电荷，是一种延申CM电荷使用键校正思想的拟合RESP电荷的方法，是在使用AM1半经验方法下的Mulliken电荷的基础上，通过键电荷校正(BCC)得到。校正参数依赖键类型和两端原子类型，校正参数拟合自2755个在HF/6-31F*精度下计算的有机小分子的RESP电荷。再如MMFF94电荷模型，同样使用键电荷校正过程，但是MMFF94力场的初始电荷使用规则初始化，比如质子化氨基的N初始带+1.0电荷，去质子化的羧基的2个O各带-0.5电荷，然后使用键校正参数进行校正，校正参数来自于拟合HF/6-31G*下计算的分子偶极矩及相互作用能获取。还有应用电负性均衡原理构建的Gasteiger电荷和QEq电荷，这两种电荷的静电势复现效果较差，不再作详细介绍。

下表对常用的通用小分子力场和推荐电荷模型进行一个总结：

力场	电荷模型	ESP复现RRMSE	偶极复现MUE
-	Merz-Kollman	0.104	0.03
GAFF	AM1-BCC	0.208	0.25
GAFF	RESP	0.141*	-
OPLS	1.14*CM1A-LBCC	0.268(CM2)	0.35(CM2)
CGenFF	CGenFF	-	-
MMFF94	MMFF94	0.252	0.36
Tripos	Gasteiger	0.561	0.68
UFF	QEq	0.532	1.03

评测数据来源于文献《原子电荷计算方法的对比》各电荷模型与HF/6-31G*级别计算静电势或偶极的比较，CM系列电荷模型的评测使用CM2电荷，*RESP评测数据来源于AM1-BCC电荷文献。

ESP和RESP电荷计算方法

化学分子多静电势由原子核电荷和电子密度两部分构成：

$$\begin{array}{cc} V_{ESP}(r) = &\sum_k^{nuclei} \frac{Z_k}{|r-r_k|} &-\int dr'\Psi^*(r')\frac{1}{|r-r'|}\Psi(r') \\\\ \mathrm {静电势}=& \mathrm {核效应} & \mathrm {-电子效应} \end{array} \tag{4.1}$$

对于核区，总是由核效应主导，对于体系范德华表面，由核效应和电子效应共同决定，可正可负，具有明显的化学意义，与分子间的的相互作用直接相关。因此可在分子范德华表面及表面外的一定区域取一批格点$V_i$，通过最小二乘法拟合原子的偏电荷。

首先RESP电荷与ESP电荷(MK电荷或CHELPG电荷)一致，通过量化软件在至少HF/6-31G*级别下计算分子范德华表面格点的静电势，每个静电势格点的静电势数值记为$V_i$。假设我们已经在每个原子上拟合了偏电荷$q_j$，根据经典库仑公式，可以计算格点上的拟合静电势$E_i$：

$$\tag{4.2} E_i = \sum_{j=1}^n\frac{q_j}{r_{ij}}$$

其中$n$为分子的原子数，$r_{ij}$为格点到原子的距离。因此我们的目标就是最小化每个格点的静电势差，即优化目标：

$$\tag{4.3} \min(\sum_i(E_i-V_i)^2)$$

因此可用最小二乘法求解：

$$\tag{4.4} f(q) = \sum(E_i-V_i)^2$$

即另$f{q}$的一阶导${\mathrm{d} f(q)} / {\mathrm{d} q} = 0$，求解q。

省略一阶导的展开过程，接下来我们通过构造矩阵求解最小二乘法的解。

设矩阵A为：

$$\tag{4.5} A_{jk}=\sum_{i=1}^m\frac{1}{r_{ij}r_{jk}}$$

设向量B为：

$$\tag{4.6} B_{k}=\sum_{i=1}^m\frac{V_i}{r_{ik}}$$

其中$m$是格点数。$A$是一个$n \times n$矩阵，$B$是一个$n$个元素的向量。$r_{ij}$为第i个静电势格点到j个原子的距离，$r_{ij}$为第i个静电势格点到k个原子的距离。

则可通过最小二乘法的矩阵运算：

$$\tag{4.7} \text{Aq-B=0} \quad => \quad \text{q}=(\text{A}^T\text{A})^{-1}\text{A}^T\text{B}$$

求向量$q$，$q$是n纬向量，即n个原子对应的偏电荷。

为了限制拟合后的各原子偏电荷的加和与分子净电荷一致，在矩阵A增加一行全为1的向量，向量B的最后一个元素添加分子净电荷$Q$，即可限制净电荷一致。

$$\tag{4.8} \sum_j^nq_j=Q \\\\ => \begin{bmatrix} 1 & 1 & \cdots & 1 \end{bmatrix} \times \text{q} = Q$$

此时我们获得ESP电荷。但是ESP电荷仍有很多问题，比如分子表面原子对表面静电势影响大，分子内部的原子则影响小，因此表面电荷会偏大；再如构象不同，ESP电荷也会变化。RESP电荷通过添加双曲函数限制来优化这两个问题。

接下来我们添加限制条件。首先保证化学环境相同原子，如乙基的两个H原子，的偏电荷相等：

$$\tag{4.9} q_j-q_k=0$$

与净电荷限制类似，我们在矩阵A增加一行，令此行j和k原子对应的位置为1和-1，其余位置为0。同时在向量B添加一个为0的元素，即添加上式电荷相等限制。其余对称原子重复以上步骤。

双曲函数限制通过对矩阵A的对角元素$A_{jj}$添加限制参数：

$$\tag{4.10} A_{jj} = \sum_i\frac{1}{r_{ij}^2}+aq_j(q_j^2+b^2)^{-1/2}$$

参数$a$代表限制强度，$b$代表双曲线极小点的紧凑程度。一般$b$设为$0.1 e$，$a$在两步RESP拟合中分别设为$0.0005 a.u.$和$0.001 a.u.$。

RESP方法推荐两步拟合，第一步$a$使用较宽松的$0.0005 a.u.$，而且不开启对称限制，这样可以对极性片段进行较好地拟合；第二步将极性原子的电荷固定，固定方法与净电荷限制方法类似（基本只对烷基的H原子开启对称限制），$a$使用较严格的$0.001 a.u.$，来进行优化。

RESP电荷的计算方法和Python代码实现可见CSD Group为Psi4开发的RESP方法的论文和相应代码Git仓库。

AM1-BCC电荷计算方法

AM1-BCC电荷是一种受到CM系列电荷启发的近似RESP电荷模型的方法。CM电荷提出一种“键电荷增长”(Bond Charge Increment, BCI)方法，对低级别方法下的Mulliken或Löwdin电荷进行键较正，如CM2对AM1、PM3、HF/MIDI!、HF/6-31G*的Löwdin电荷分别拟合了校正参数。

CM2校正电荷计算公式为：

$$\tag{4.11} q_i^{CM2} = q_i^{\text{Löwdin}}+\sum M_{i,j}(D_{i,j}+C_{i,j}M_{i,j})$$

其中$M_{i,j}$为i和j原子间化学键的Mayer键级，$C$和$D$是对实验气相偶极矩拟合的经验参数，取决于化学键的种类。

AM1-BCC在CM电荷的思想下提出几点改进，首先是不再以偶极矩为拟合目标，而是HF/6-31G*级别静电势，其次是简化BCC方法，不使用Mayer键级而是规则键，这种校正方法被AM1-BCC方法取名为“键电荷校正”(Bond Charge Correction, BCC)方法。

AM1-BCC校正电荷计算公式为：

$$\tag{4.12} q_i^{AM1-BCC} = q_i^{\text{AM1}}+\sum_{\alpha=1}^{\gamma_i} (BCC_{\alpha(i->j)})$$

$\gamma_i$为原子i连接的原子数或化学键数，$BCC_{\alpha}$为原子i的化学键${\alpha}$的BCC校正参数，校正参数的符号与键的方向一致，如C-H键的C需要加上BCC_C->H，C-H键的H需要减去BCC_C->H。

与CM方法类似，AM1-BCC电荷对多个半经验方法的Mulliken电荷模型都尝试进行键电荷校正，通过对EHT(Extended Hückel Theory)方法，或半经验方法MNNDO，AM1，PM3获得的Mulliken电荷进行参数化。EHT方法电荷模型无法有效复现HF/6-31G*级别的静电势，而MNNDO，AM1，PM3等半经验方法结果几乎一致，因此该方法选择被多种量化软件广泛支持的AM1方法作为推广方法。

BCC校正参数拟合可通过最小二乘法的矩阵形式求解，具体求解过程见论文Inc. J Comput Chem 21: 132–146, 2000。以下为简述版本。

设矩阵A为：

$$\tag{4.13} A_{\beta \alpha} = \sum_{l=1}^{M} \sum_{k,j=1}^{N} \sum_{\beta=1}^{\gamma} \frac{T_{\beta k}T_{j\alpha}}{r_{kl}r_{lj}}$$

设向量B为：

$$\tag{4.14} B_{\beta}=\sum_{l=1}^M \sum_{k=1}^N \frac{T_{\beta k}T_{j \alpha}}{r_{kl}}$$

其中$l$为ESP格点索引，$\alpha$和$\beta$为BCC校正索引，$j$和$k$为原子索引，$T$为每个原子拥有的BCC键连关系类型，维度为原子数xBCC校正数。

即求解方程：

$$\tag{4.15} \text{Ap-B=0} \quad => \quad \text{p}=(\text{A}^T\text{A})^{-1}\text{A}^T\text{B}$$

可得p为$\gamma$维向量，$\gamma$即BCC校正参数的数量，p即BCC校正参数列表。

表4.2 BCC校正参数（节选） -: 单键 =: 双键 ≡: 三键

校正类型	训练集数量	校正参数	校正类型	训练集数量	校正参数
C.sp3-C.sp3	1876	0.0000	C.sp3-H	10885	0.0393
C.sp3-O.sp3	750	0.0718	O.sp3-H	386	-0.2010
O.sp2-S.sp3	385	0.2792	C.sp3-N.sp3	860	0.1528
C.sp2=C.sp2	613	0.0000	C.sp3-F	123	0.0713
C.sp≡N.sp	160	0.3258	C.sp3-Cl	147	0.0734
C.sp2=O.sp2(酮)	115	0.1890	C.ar-Br	4	0.1401
C.sp2=O.sp2(酸)	301	0.2391	C.ar-I	4	0.2859

根据表4.2，甲醇的C原子电荷需要在AM1电荷基础上增加$3 \times 0.0393 + 1 \times 0.0718=0.1897\,(e)$，O原子电荷需要在AM1电荷基础上增加$1 \times (-0.2010) + 1 \times (-0.0718) = -0.2728\,(e)$。

AM1-BCC电荷的训练数据使用了由H, C, N, O, F, Si, P, S, Cl, Br和I原子组成的2,755个有机小分子。评测结果表明AM1-BCC电荷的表现优于MMFF94电荷模型，接近RESP电荷，因此凭借极低的计算消耗和较高的精度，AM1-BCC电荷成为GAGG力场的除RESP外的可选电荷之一。

总结

本文第一部分描述了分子力场中的几种电荷模型，如RESP，AM1-BCC，CM2，MMFF94等，以及基于静电势复现思想的电荷模型是分子力场的最佳电荷模型。本文第二部分描述了RESP电荷和AM1-BCC电荷的拟合方法和参数优化方法。RESP电荷是AMBER和GAFF的御用力场模型，对静电势拟合极好，且能极大地规避多构象和分子内原子电荷屏蔽的问题。AM1-BCC电荷应用CM2电荷的BCI思想，提出了在便宜的AM1电荷上通过键电荷校正BCC来接近RESP的表现。AM1-BCC和RESP电荷都是AMBER/GAFF力场的推荐电荷，AMBER力场的生物大分子如氨基酸和核苷酸使用HF/6-31G*级别的RESP电荷模型，GAFF小分子力场推荐RESP电荷，可选AM1-BCC电荷，AmberTools可调用SQM程序单独完成AM1-BCC电荷计算。

AM1-BCC电荷也存在一些缺陷，比如AM1-BCC电荷模型没有B元素或金属离子配位键的电荷参数，部分键连关系如芳环C和卤素连接在训练集中数据量较少，以及对孤电子对或Sigma Hole的电子效应无法计算，AM1-BCC是气相模拟结果与凝聚相模拟存在误差等。碰到此类问题可以通过RESP电荷模型计算，RESP电荷与化学元素关系极小，也可通过添加虚原子模拟孤电子对或Sigma Hole，RESP2思想则是对凝聚相的优化。但是RESP的计算成本远高于AM1-BCC，半经验方法近年来也有长足发展，因此新的AM1-BCC电荷模型的拟合参数也亟待更新发展。