定制小分子力场(二)：从通用力场到GAFF

引言

在上一篇文章中我们了解了AMBER力场中的函数类型，根据我们所知，分子力场由函数形势和力场参数组成，本文将详细介绍GAFF小分子通用力场中如何描述不同化学环境中原子的力场参数。

通用小分子力场

General AMBER Force Field (GAFF)即通用AMBER力场，是一套针对有机小分子的通用力场参数。除GAFF外，通用小分子力场还有兼容CHARMM力场的CGenFF，OPLS力场系列的OPLS-AA、OPLS4，开源通用小分子力场OpenFF，以及MM系列小分子力场和MMFF94力场，和全周期通用力场UFF。CGenFF力场需要在线服务器，OPLS-AA也需要在线生成，OPLS4则是薛定谔公司的商业版OPLS力场，获取都较为困难。MM和MMFF94参数复杂，无法通过Gromacs或Amber程序运行分子动力学模拟，UFF力场则较为粗糙，一般也不用于小分子动力学模拟，而且这两类力场也没有兼容的生物大分子力场。OpenFF和GAFF都可以通过离线软件完成参数构建，且都兼容AMBER的生物大分子力场，甚至OpenFF的更新更频繁，理念更先进，但是也偶尔会有软件运行中的bug问题。而GAFF力场虽然研发缓慢（十年只缓慢更新了一个大版本GAFF2），但相对简并的参数也提高了程序运行的稳定性。接下来我们将详细介绍GAFF力场的参数文件。

从药化角度设计一个通用力场

本教程希望是一个简单和渐进的力场教学，因此我们从基础的药化知识开始构建一个力场。假设我们要给烷烃化合物设计一个力场，那么最简单的情况是定义两种原子类型，C和H，并且设定两类原子的范德华参数$\epsilon$和$\sigma$。设定两种键长参数C-H和C-C的$k_l$和$l_0$，三种键角关系C-C-C，H-C-H，H-C-C的$k_\theta$和$\theta_0$，以及三种二面角关系C-C-C-C，H-C-C-H，H-C-C-C的周期$N$和相位$\omega$和振幅$V_n/2$。这样我们就获得了一个描述饱和烷烃的简单力场（除库仑项）。这里要注意，原子电荷是需要单独拟合的，我们在后续文章中再进行讲解。

图1.1 TRIPOS力场原子类型示意图

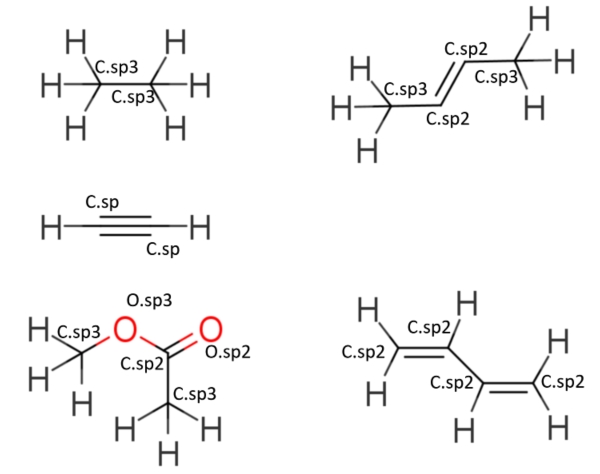
假如我们不满足饱和烷烃，希望能够模拟含有双键的烯烃，那么首先我们需要定义新的键连关系，因为烯烃的双键两侧不可旋转，且双键键长比单键短，双键的平衡常数k增加和平衡距离l缩短。那么我们就无法使用C-C描述烯烃键伸缩参数，我们给烯烃的C进行单独命名，比如C.sp2，烷烃的C改为C.sp3。这样我们描述通用烯烃的力场就是三种原子类型C.sp3, C.sp2, H和对应的范德华参数，三种键长参数C.sp3-H，C.sp3-C.sp3，C.sp3-C.sp2，C.sp2-H，十一种键角关系C.sp3-C.sp3-C.sp3, C.sp2-C.sp3-C.sp3，C.sp2-C.sp2-C.sp3，C.sp2-C.sp2-C.sp2，C.sp3-C.sp2-C.sp3，H-C.sp3-H，H-C.sp2-H，H-C.sp2-C.sp2，H-C.sp3-C.sp3，H-C.sp2-C.sp3，H-C.sp3-C.sp2，以及更多的二面角关系。

目前我们可以描述烷烃和烯烃，但是像炔烃、醚，酰胺、饱和环和芳环，仍然缺失参数。可以根据前文的规律，我们可以继续定义比如C.sp2，O.sp3，O.sp2，O.amide，N.sp3，N.sp2，C.ar，N.ar，C.ar等原子类型和对应范德华参数，再补充对应的键长、键角、二面角参数，就可以描述除了库仑项外的所有力场参数。这里提到的命名方法，如C.sp2，读者如果经常使用MOL2文件的话，可以在MOL2文件中看到这类原子类型，这其实就是是TRIPOS力场中的原子类型，MOL2也是TRIPOS力场的官方格式。TRIPOS力场也是一种通用小分子力场，主要用作Sybyl对接软件的对接力场，目前已经不再更新。

似乎我们很轻松的搭建了一个通用力场框架，但实际上还有几个问题没有解决。第一个问题是原子类型是否完备。比如使用上面的原子类型C.sp3和C.sp2描述1,3-丁二烯，2号和3号C原子之间的键连关系如果归属为C.sp2-C.sp2，则会错误地将单键描述为烯烃双键，实际上述1,3丁二烯的2号和3号C原子之间是存在部分双键性质的单键，那么我们应该至少再添加一类原子，来描述通过单键连接一个C的烯烃C。TRIPOS力场中有约60中原子类型，OPLS-AA中原子类型则超过800种。

第二个问题是原子类型增加带来参数爆炸。假如原子类型有N种，键连关系类型理论上限$A_N^2$，键角关系类型理论上限$A_N^3$，二面角关系类型理论上限$A_N^4$，导致了参数数量的组合爆炸。力场处理组合爆炸的方法将从在下文中逐步阐明。

GAFF力场

GAFF力场的参数库文件一共有两个，用于定义原子类型的GAFF.prm，和用于定义力场参数（范德华参数，键长，键角，二面角，异二面角）的GAFF.dat。

GAFF中的原子定义 GAFF.prm

在GAFF力场的GAFF.prm中，所有的原子类型都是小写，比如c1（SP杂化C），c2（SP2杂化C），c3（SP3杂化C），因为大写的原子类型如C，O，CT等用于描述蛋白和核酸等生物大分子，借此以作区分。

Table 2.1 GAFF 力场中的C原子类型

AtomType	Description	AtomType	Description
c	C=O, C=S中的sp2 C	c1	sp1 C
c2	sp2 脂肪C	c3	sp3 C
ca	sp2 芳香C	cc(cd)	环体系中的共轭体系的内侧sp2 C
ce(cf)	链体系中的共轭体系的内侧sp2 C	cp(cq)	联苯中的桥接C
cu	三元环中的sp2 C	cx	三元环中的sp3 C
cv	三元环中的sp2 C	cy	三元环中的sp3 C
cg(ch)	链/环体系中的共轭体系的内侧sp1 C	cz	胍基C

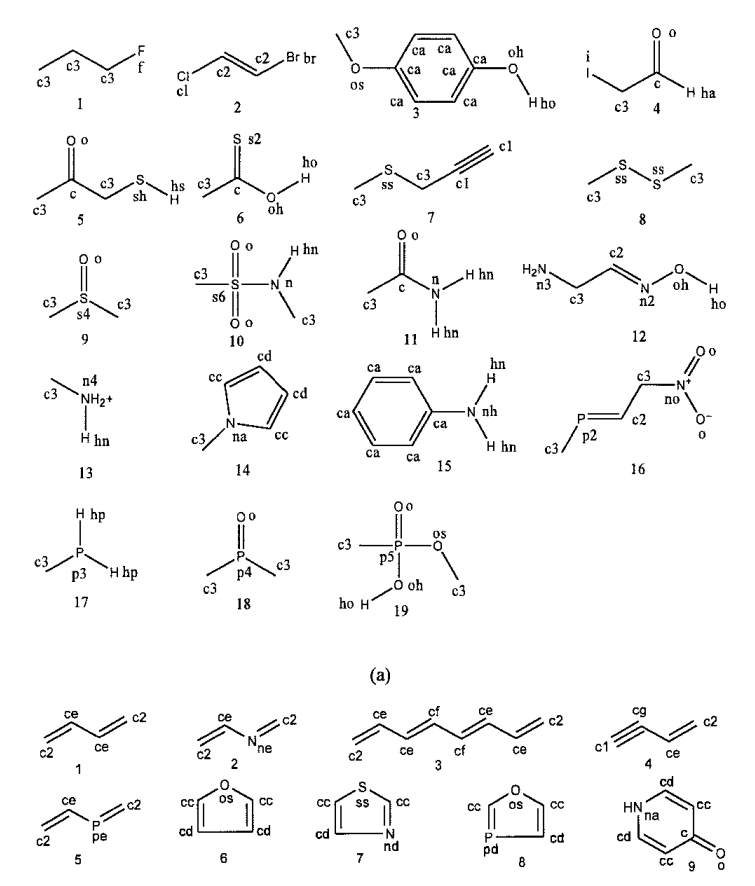
在GAFF力场中，我们有了更多的原子类型来解决前文中的1,3-丁二烯问题。如图所示，1,3-丁二烯的两个末端C的原子类型为c2，即表2.1中所述sp2 C，2号和3号C的原子类型被定义为ce，，即表2.1中所述链体系中的共轭体系的内侧sp2 C，这样定义后c2-c2的键参数和ce-ce键参数就可以正确区分开。

图2.2 GAFF力场原子类型示意图

读者可能注意到，原子类型cc旁还有一个括号内的cd原子类型，这个原子类型事实上是GAFF力场中十分精妙的原子分类，即用于处理重复的共轭体系。比如已三烯或辛四烯，中间的烯键两侧的C都属于“的共轭体系的内侧sp2 C”这一范畴，如果都使用cc这一原子类型，那么就会有三根ce-ce键存在，其中两根是单键，一根是3,4原子间的双键。为了解决这类问题，引入与ce相同但命名不同的cf原子类型，定义ce-ce键等同cf-cf键，为共轭烯烃的单键，定义ce-cf键等同c2-c2键，为共轭烯烃的双键。这样就可以区分带有重复片段的共轭体系。

在GAFF力场的GAFF.prm中使用SMARTS语言定义原子类型，SMARTS语言是SMILES语言的类正则拓展，是一种线性的化学结构描述语言，可以景区定义原子、片段、或分子。我们截取一段GAFF2.prm文件中对几类C原子类型的定义进行解读：

// GAFF2.prm
...
// SMARTS rules for carbons

atom [c]								    ca "sp2 C in aromatic ring"
atom [#6X3;R](=[#6,#7,#8])(-[#6,#7,#8])(-[#1])				    ca "sp2 C in aromatic ring"
atom [#6X3;R](:[#6])[#6] 						    ca "sp2 C in aromatic ring"
atom [#6X3;R](=[#6])([#6])[#1]						    ca "sp2 C in aromatic ring"
atom [#6X3;R](=*)-*=*   						    ca "sp2 C in aromatic ring"
atom [#6X3;R](=[#6X3])([#6])[#1]					    ca "sp2 C in aromatic ring"	
...
atom [#6X3;!R](=[*&!O,S])-*=*   					    ce "sp2 C conjugated chain"
atom [#6X3;!R](#*)-*=*   						    ce "sp2 C conjugated chain"
atom [#6X3;!R](#*)-*#*   						    ce "sp2 C conjugated chain"
atom [#6X3;!R](=*)-*#*   						    ce "sp2 C conjugated chain"
atom [#6X3;H&!R](=*)-*~[R;a] 						    ce "sp2 C conjugated chain"
...
atom Please try to write SMARTS       					    cz "guanidine carbon"
...

文件中//代表注释，每一行代表一个原子定义，第一列为固定的提示词atom，第二列为具体的SMARTS定义，第三列为原子类型，最后一列以双引号括住的是原子类型的具体释义。我们以ca原子类型的前两行坐下解释。[c]小写的c即芳香C，对于芳香式存描述的C用这种写法就可以匹配，凯库勒式描述的芳香C略显麻烦，见下一行[#6X3;R](=[#6,#7,#8])(-[#6,#7,#8])(-[#1])，这里使用了SMARTS的递归写法，意思是匹配“一个有三个连接原子的单环上的C，其中一个通过单键连接C,N,O原子，另一个通过双键连接C,N,O原子，最后一个通过单键连接H原子”。另外还有几种ca的描述进行了更细枝末节的补充，前文提到的ce我也截取出供读者参考。匹配胍基的C的cz则留给读者做SMARTS练习。

GAFF中的力场参数 GAFF.dat

GAFF力场的GAFF.prm文件仅存储了原子定义，另一部分的具体的力场参数存储在GAFF2.dat文件中。GAFF.dat格式与Amber的.dat文件格式基本一致，只是略有不同。

图2.3 GAFF.dat文件的组成部分

原子类型和范德华参数部分

第一部分原子类型和第五部分范德华参数内容排布基本一致，都是归属到原子的性质。比如第一部分，每一行都是一种GAFF原子类型和对应的原子质量和可极化参数，这两个参数主要用在Amber程序中，Gromacs不需要极化参数，且原子质量通过元素类型可以直接指定。

原子类型   分子量  可极化参数   原子类型解释
c  12.01         0.616               Sp2 C carbonyl group 
c1 12.01         0.360               Sp C
c2 12.01         0.360               Sp2 C  
c3 12.01         0.878               Sp3 C
ca 12.01         0.360               Sp2 C in pure aromatic systems
...

第五部分数据有四列，第一列为原子类型，第二列为范德华半径$r_0$，单位$\text{\AA}$，第三列为势阱深度$\epsilon$，单位为$kcal/mol$，最后一列为参数来源。$r_0$向$\sigma$的转换可以参考上一篇文章，使用公式$\sigma=2^{(-6/5)}r_0$进行转换。

原子类型  范德华半径R0  势阱深度E  参数来源说明
  c1          1.9080  0.2100             cp C DLM 11/2007 well depth from OPLS replacing 0.0860
  c2          1.9080  0.0860             sp2 atom in the middle of C=CD-CD=C
  c3          1.9080  0.1094             OPLS
  ca          1.9080  0.0860             OPLS
  cc          1.9080  0.0860             OPLS
  cd          1.9080  0.0860             OPLS
  ce          1.9080  0.0860             OPLS
  cf          1.9080  0.0860             OPLS
...
  ss          2.0000  0.2500             W. Cornell CH3SH and CH3SCH3 FEP's
  p2          2.1000  0.2000             JCC,7,(1986),230; 
...
  f           1.75    0.061              Gough et al. JCC 13,(1992),963.
  cl          1.948   0.265              Fox, JPCB,102,8070,(98),flex.mdl CHCl3
  br          2.02    0.420              Junmei, 2010
  i           2.15    0.50               Junmei, 2010

对于范德华参数的来源，第一来源是Dr.William Jorgensen的OPLS力场，其次是Dr.Peter A. Kollman的AMBER大分子力场，如JCC,8,(1992),963中的H原子参数化，JCC,7,(1986),230的P原子参数，JACS,117,(1995),19的S原子参数等。范德华参数的拟合将在后续文章中讨论，讨论为什么GAFF借用了大量OPLS的力场力场参数。

细心的读者可能会想到，范德华力发生在两个原子之间，为什么范德华参数是原子性质而不是原子对性质。这是因为原子间的范德华参数通过算术或几何平均获取，如AMBER和GAFF力场使用Lorentz-Berthelot规则，$\sigma$使用算术平均计算，$\epsilon$使用几何平均计算：

$$\tag{2.1} \sigma_{ij} = \frac{1}{2}(\sigma_{ii} + \sigma_{jj}) \\ \epsilon_{ij} = (\epsilon_{ii} \epsilon_{jj})^\frac{1}{2}$$

或像OPLS力场全部使用几何平均计算：

$$\tag{2.2} \sigma_{ij} = (\sigma_{ii} \sigma_{jj})^\frac{1}{2} \\ \epsilon_{ij} = (\epsilon_{ii} \epsilon_{jj})^\frac{1}{2}$$

键长和键角参数

GAFF1键长参数共791，第一列为成键原子类型对，第二列为力常数，单位kcal/mol，第三列为平衡键长，单位nm，第四列为参数来源，其余后列为测试数据量和 测试误差RMSD。

成键原子类型对  力常数  平衡键长 参数来源  测试数据量  测试误差RMSD
ow-hw  553.0    0.9572       TIP3P_Water   1	
br-br  123.2    2.5420       SOURCE1       4	0.0000
br-c1  352.7    1.7870       SOURCE2       4	0.0024
br-c2  278.7    1.8830       SOURCE1      31	0.0000
br-c   240.3    1.9460       SOURCE2       2	0.0285
br-c3  229.5    1.9660       SOURCE1     100	0.0000
br-ca  269.6    1.8970       SOURCE1     127	0.0058
br-cc  277.6    1.8847       SOURCE4      39	0.0068
br-cx  261.4    1.9100       SOURCE1       8	0.0000
br-i   142.4    2.6710       SOURCE1       2	0.0245
br-n1  330.4    1.8600       SOUECE3       1	
br-n2  219.0    2.0380       SOURCE3       5	0.1082
br-n   320.2    1.8730       SOURCE3       4	0.0046
br-n3  265.9    1.9520       SOURCE3       2	0.0000

GAFF1键角参数共4071，第一列为成角原子类型对，第二列为力常数，单位kcal/mol，第三列为平衡角度，单位°，第四列为参数来源，其余后列为测试数据量和 测试误差RMSD。

成角原子类型对  力常数  平衡角度 参数来源  测试数据量  测试误差RMSD
hw-ow-hw   42.730     104.520	AMBER              1	TIP3P_water
hw-hw-ow    0.000     127.740	AMBER              1	(found_in_crystallographic_water_with_3_bonds)
br-c1-br   57.760     180.000	Guess              0	
br-c1-c1   54.930     180.000	SOURCE3            1	0.0000
c1-c1-c1   64.410     180.000	SOURCE3            1	0.0000
c1-c1-c2   60.840     180.000	SOURCE3            2	0.0000
c1-c1-c3   56.280     178.460	SOURCE4          188	0.6631
c1-c1-ca   56.920     180.000	SOURCE3            1	
c1-c1-cl   55.270     180.000	SOURCE3            1	
c1-c1-f    61.020     180.000	SOURCE3            1	

平衡键长参数来源主要有4个：1. J. Chem. Soc., Perkin Trans. 2, 1987, S1-S19中的X射线晶体衍射结构，2. J.Phys Chem Ref Data., 8, 1979, 619-722中的X射线晶体衍射结构，3. MP2/6-31G*级别优化结构，4. B3LYP/6-31G*级别优化结构。

$$\tag{2.3} v=\frac{1}{2\pi c}\sqrt{\frac{k}{\mu}}, \quad \mu=\frac{m_im_j}{m_i+m_j}$$

力常数参数来源主要有3个：1. 实验测定的波数$v$，经过波数公式可以计算得到的力常数，其中$c$为光速/波速，$mu$为约化质量，$k$为力常数；2. MP2/6-311G+(d,p)级别量化计算得到的振动频率乘缩放系数0.9496后计算的力常数；3. 根据前两种高精度放法计算的力场数，使用Badger规则和线性回归拟合的其他键的力常数。

前两种来源比较直观，第三种来源类似于MAFF94力场，即使用高精度的力场参数补全未知的力场参数。比如对键角来说，$\Theta_{(A-B-C)}$的键角大小可以通过$\Theta_{(A-B-A)}$和$\Theta_{(C-B-C)}$的平均得到，力常数则使用经验公式根据(A-B-C)原子类型拟合。

如公式：

$$\tag{2.4} K_{ij}^l=\frac{K_{ii}|r_{ij}^{ref}-r_{jj}^{ref}|-K_{jj}|r_{ij}^{ref}-r_{ii}^{ref}|}{|r_{ij}^{ref}-r_{jj}^{ref}|-|r_{ij}^{eq}-r_{ii}^{ref}|}\cdot \bigg(\frac{1}{r_{ij}}\bigg)^m$$

其中$r^{ref}$是参考键长，$K_{ij}$是经验参数，$m$是幂数，在MMFF94中$m$是常数6，GAFF做了广义推广，可以是不同的实数。部分参数，如H，C，N，O元素的$K_{ij}$见：

$i$	$j$	$r_{ij}^{ref}$	$lnK_{ij}$
H	H	0.738	4.661
C	C	1.526	7.643
N	N	1.441	7.634
O	O	1.460	7.561
S	S	2.038	8.316

及公式：

$$\tag{2.5} K_{ijk}^\Theta=143.9C_iZ_jC_k(r_{ij}^{eq}+r_{jk}^{eq})^{-1}(\Theta_{ijk}^{eq})^{-2}exp\bigg(-2\frac{(r_{ij}^{eq}-r_{jk}^{eq})^2}{(r_{ij}^{eq}+r_{jk}^{eq})^2}\bigg)$$

其中$C_iZ_jC_k$分别是(A-B-C)原子的拟合来的经验参数，$\Theta^{eq}$是平衡键角。GAFF中的全部$C_iZ_jC_k$数值见下表：

Element	C	Z	Element	C	Z
H	-	0.784	Cl	-	1.272
C	1.339	1.183	Br	-	1.378
N	1.300	1.212	I	-	1.398
O	1.249	1.219	P	0.906	1.620
F	-	1.166	S	1.448	1.280

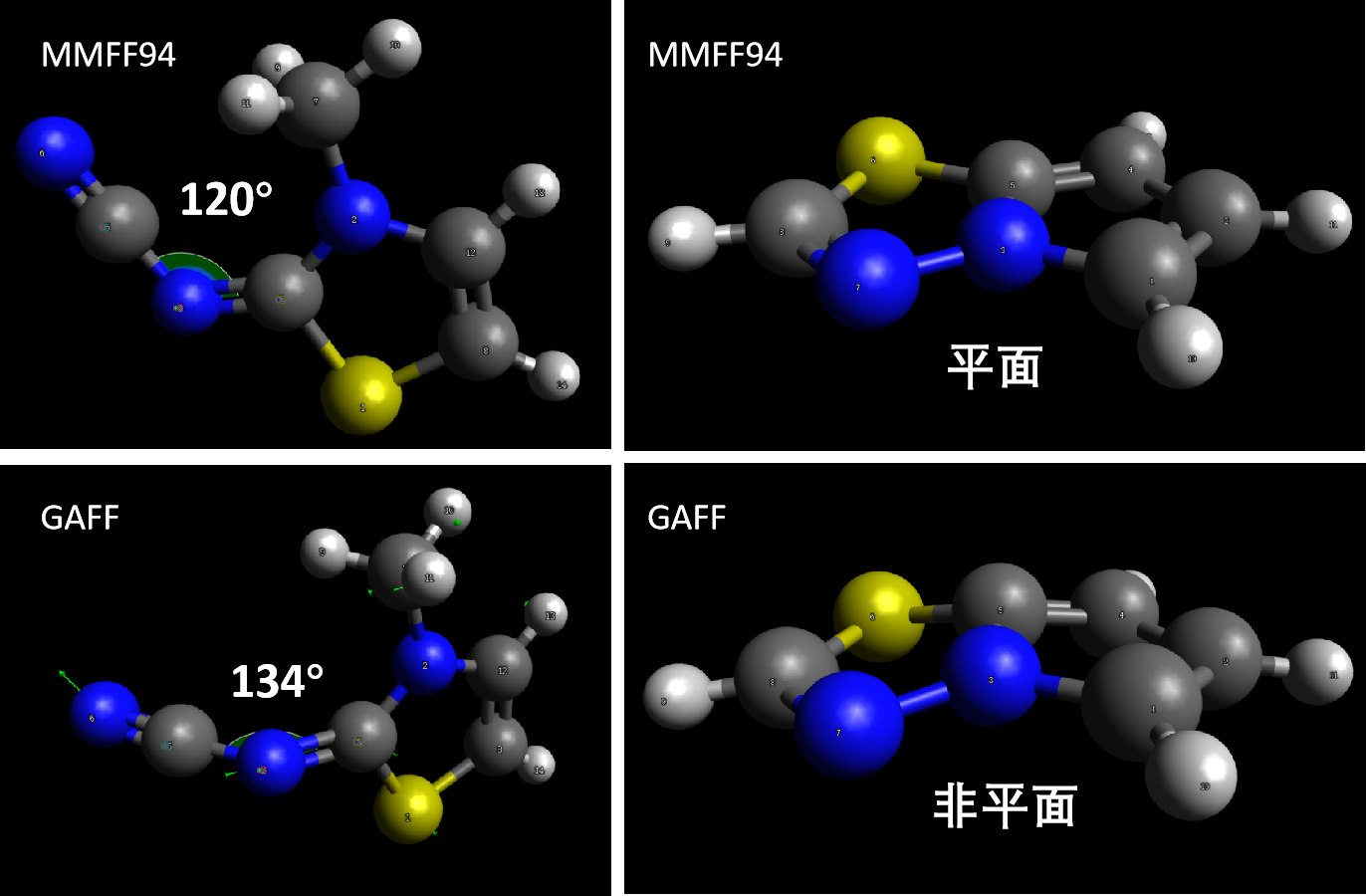
尽管使用高精度的力场参数补全未知的键长键角力场参数，极大节省了计算量，但是这种组合办法仍然是有风险的，特别是对键角的影响。举例来讲，对于6并6的芳香体系，每个重原子X-X-X键角都是120°，而对于5并5的芳香体系，每个重原子X-X-X键角应该接近108°，但是GAFF的组合方法可能仍会给5并5体系的X-X-X键角120°的平衡角度，最终结果会导致5并5芳香体系的平面发生折叠。

图2.4 GAFF力场优化构象出现的键角错误样例

二面角和异二面角参数部分

GAFF.dat种二面角参数如下：

二面角参数
成二面角原子类型对  除数因子  势垒高度x除数因子  相位  周期 参数来源等
X -c -c -X    4    1.200       180.000           2.000
X -c -cg-X    2    0.000       180.000           2.000      same as X-c-c1-X 
X -c -ch-X    2    0.000       180.000           2.000     
X -c -c2-X    4    8.700       180.000           2.000      intrpol.bsd.on C6H6
X -c -cu-X    4    8.700       180.000           2.000      intrpol.bsd.on C6H6
X -c -c3-X    6    0.000       180.000           2.000      JCC, 7, (1986), 230
X -c -cx-X    6    0.000       180.000           2.000      JCC, 7, (1986), 230
X -c -cc-X    4   11.500       180.000           2.000      statistic value 
...
X -n2-ss-X    1    2.800       180.000          -2.000
X -n2-ss-X    1    1.300       180.000           1.000
X -ne-ss-X    1    2.800       180.000          -2.000
X -ne-ss-X    1    1.300       180.000           1.000
X -nf-ss-X    1    2.800       180.000          -2.000
X -nf-ss-X    1    1.300       180.000           1.000
...
异二面角参数
X -o -c -o          1.1          180.          2.           JCC,7,(1986),230
X -X -c -o          10.5         180.          2.           JCC,7,(1986),230
X -X -ca-ha         1.1          180.          2.           bsd.on C6H6 nmodes
...

GAFF二面角参数共714个，异二面角参数38个。第一列为成二面角原子类型对，第二列为除数因子，第三列势垒高度x除数因子，单位$kcal/mol$，第四列相位，单位°，第五列周期，第六列参数来源。相比于键角参数接近5000个，多一个原子的二面角参数反而下降到700个左右，原因在于大部分二面角参数都采用类似X -c -c -X 描述二面角类型，其中X代表通配原子，即不考虑两侧原子，二面角主要由中间化学键类型决定，其次由1，4原子之间的弱相互作用决定。因此尽管都使用二面角参数X -c -c -X ，h -c -c -h 和c -c -c -c 的键旋转能仍然会有差异，显然c -c -c -c 的1,4相互作用的斥力更大，旋转时的能垒会更高。使用这种通配符式的二面角参数的主要目的就是节省开发力场的计算量，避免数据组合爆炸，缺点也较为明显，对部分特殊二面角无法正确描述。

异二面参数用于维持环体系的平面性，通常使用一个较小的力常数如GAFF力场中的1.1 kcal/mol足够，偶尔需要高能力场数如10.5 kcal/mol，高能力常数可能会导致高频振荡，因此一般不适用。异二面角参数作为经验参数，具体的势垒一般也没有具体物理意义，基本是猜测一个小的势垒维持稳定即可。

二面角参数主要来源于对200个模式片段二面角进行MP4/6-311G(d,p)//MP2/6-31G*级别的量化扫描后，使用Pharmscan软件进行拟合获得势垒，周期和相位。大部分的二面角参数使用一组参数描述，少部分复杂参数用到两组或三组，在GAFF.dat种，如果第五列的周期数为负值，则说明需要额外读取下一行另一组参数，这里的负号仅作为额外参数提示，实际周期取正值。还有一些参数来源于AMBER98力场，注释列都有引用。

补充

从GAFF发表开始，GAFF力场也在逐渐更新中。GAFF.dat文件记录了历次GAFF力场向GAFF2力场更新过程中的工作内容，比如针对前文所述的五元芳环平面性问题，UCSF的Dr. Gabriel Rocklin提议使用cc(cd)类型描述（实际上对于5并5芳环仍然没有解决平面性问题），Dr. David Mobley在优化FEP计算结果时优化的c1，cg，ch原子的范德华参数，GAFF开发者Dr. Junmei Wang本人基于CH3Br和CH3I的实验密度而对Br和I原子的范德华参数优化，以及使用超过1万5千药物或生物活性分子的B3LYP/6-31G*级别量化优化后的键长键角数据的重新拟合，分别优化了59个低质量键长参数和437个键角参数，例如图2.4中的5并5的平面性问题在这里基本得解决。