定制小分子力场(一)：分子力场基础

引言

分子力场描述分子之间相互作用的势能与力。分子动力学模拟则通过分子力场逐步更新分子体系中所有原子的势能、速度和坐标，描述特定条件下的分子运动，从而获取我们关注的模拟体系微观或宏观信息。本博客将通过一系列文章以General Amber Force Field(GAFF)小分子通用力场为例，详细讲述小分子力场的的组成与拟合，对认识分子力场与分子力场优化提供一份基础教程。本篇内容作为开篇，将介绍分子力场的基础信息。

本文将以AMBER力场和Gromacs ITP文件格式为例，进行力场的介绍。之所以使用这样的组合，是因为AMBER力场几乎所有的力场搭建工具都打包在开源软件AmberTools中，因此配套的GAFF不需要借助在线工具即可离线构建小分子力场；选择Gromacs的力场格式ITP则是因为ITP文件比Amber的力场格式文件prmtop更加可读。

分子力场的组成

根据波恩-奥本海默近似，一个分子的能量可以近似看作构成分子的各个原子的空间坐标的函数，每个原子都有不同的原子性质或参数。因此一套分子力场由描述原子间相互作用的函数形式和各类原子的力场参数两部分组成。

基本力场形势

以Amber力场为例：

$$\tag{1.1} V = \displaystyle\sum_{bonds} \frac{k_{l_i} }{2} (l_i-l_{i,0})^2 + \displaystyle\sum_{angles} \frac{k_{\theta_i}}{2} (\theta_i-\theta_{i,0})^2 + \displaystyle\sum_{torsions} \frac{V_n}{2} (1+cos(n\omega-\gamma )) \\ + \displaystyle\sum_{i=1}^N \displaystyle\sum_{j=i+1}^N \bigg(4\epsilon_{ij}\bigg[(\frac{\sigma_{ij}}{r_{ij}})^{12}-(\frac{\sigma_{ij}}{r_{ij}})^6\bigg] + \frac{q_iq_j}{4\pi\epsilon_0\epsilon_rr_{ij}}\bigg)$$

其中第一行是成键项，即分子内相互作用，第二行是非键项，即分子间相互作用和一部分远程的分子内相互作用。

$$\tag{1.2} V_{bonded} = \displaystyle\sum_{bonds} \frac{k_{l_i} }{2} (l_i-l_{i,0})^2 + \displaystyle\sum_{angles} \frac{k_{\theta_i}}{2} (\theta_i-\theta_{i,0})^2 + \displaystyle\sum_{torsions} \frac{V_n}{2} (1+cos(n\omega-\gamma ))$$

$$\tag{1.3} V_{nonbonded} = \displaystyle\sum_{i=1}^N \displaystyle\sum_{j=i+1}^N \bigg(4\epsilon_{ij}\bigg[(\frac{\sigma_{ij}}{r_{ij}})^{12}-(\frac{\sigma_{ij}}{r_{ij}})^6\bigg] + \frac{q_iq_j}{4\pi\epsilon_0\epsilon_rr_{ij}}\bigg)$$

前三项成键项又分为键伸缩能，键角弯曲能，二面角扭转能，后一项非键项又可以拆分为范德华作用能和库仑作用能，而范德华作用能由12次幂的斥力项和6次幂的引力项组成。

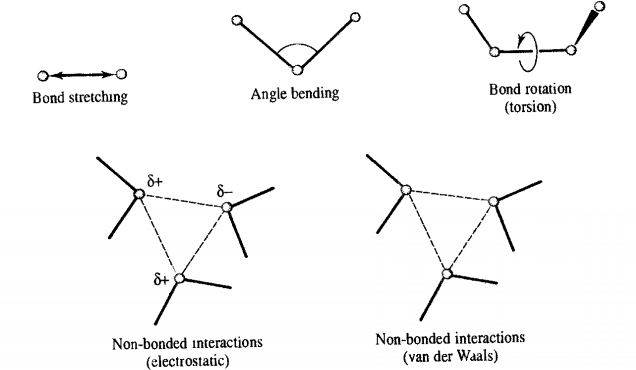
图1.1 力场中的成键项与非键项

非键项

范德华项

$$\tag{1.4} v_{vdw}=4\epsilon_{ij}\bigg[(\frac{\sigma_{ij}}{r_{ij}})^{12}-(\frac{\sigma_{ij}}{r_{ij}})^6\bigg]$$

或

$$\tag{1.5} v_{vdw}=(\frac{A_{ij}}{r_{ij}})^{12}-(\frac{B_{ij}}{r_{ij}})^6 ,A=4\epsilon_{ij}\sigma_{ij}^{12} ,B=4\epsilon_{ij}\sigma_{ij}^{6}$$

范德华项使用Lennard-Jones势能函数进行描述，其中12次项的能量符号为正值，即斥力；6次项的能量符号为负值，即引力。原子远离时6次项的引力为主导，表现出原子间的吸引，原子靠近时12次项的斥力为主导表现出原子间的排斥。

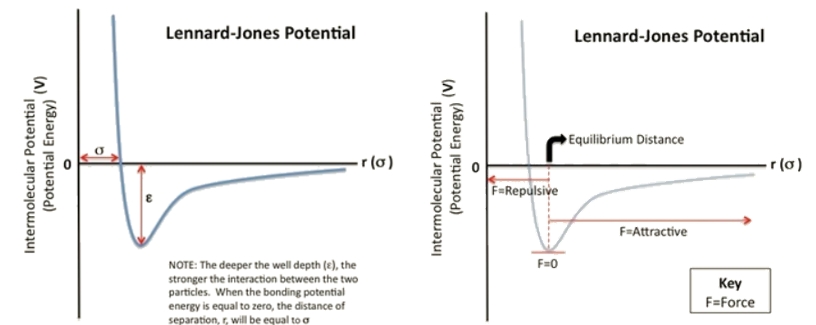
图1.2 Lennard-Jones势能函数

函数中有两个参数，$\epsilon$即势阱深度，单位为$kcal/mol$或$kJ/mol$，$\sigma$为引力斥力等值点的原子距离单位是$\text{\AA}$或nm，Amber文件格式中使用前者美标单位，Gromacs使用后者国际标准单位制。

GAFF中的F原子间的$\epsilon=0.0832 kcal/mol$，$\sigma=3.034 \text{\AA}$，当两个原子距离为$4\text{\AA}$时，原子间能量为$4*0.0832*[(3.034/4)^{12}-(3.034/4)^{6}]=-0.051kcal/mol$，当两个原子子距离为$3\text{\AA}$时，原子间能量为$4*0.0832*[(3.034/3)^{12}-(3.034/3)^{6}]=0.025kcal/mol$，当两个原子子距离为$3.034\text{\AA}$时，能量为$0$。

我们尝试求$v_{vdw}$的极小点距离，另$v_{vdw}$的导数为0，求极小点时的$r$。

$$\tag{1.6} v_{vdw}'=4\epsilon_{ij}\bigg(12\cdot\frac{\sigma_{ij}^{12}}{r_{d}^{13}}-6\cdot\frac{\sigma_{ij}^{6}}{r_d^7}\bigg)=0$$

$$=> r_d = 2^{(1/6)}\sigma \\\\ => r_0 = 2^{(-5/6)}\sigma$$

$r_d = 2^{(1/6)}\sigma$即是范德华势极小点的原子距离。回顾范德华半径的定义，我们可以直接将$r_d$除以2得到的$r_0$视作范德华半径，即F的范德华半径可近似为$1.703 \text{\AA}$。通过这种方法我们可以通过各类力场参数文件中的$\sigma$参数快速获得所需原子的范德华半径，或通过范德华半径反推$\sigma$参数。

库仑项

$$\tag{1.7} v_{coulb}=\frac{1}{4\pi\epsilon_0}\frac{q_iq_j}{\epsilon_rr_{ij}}$$

库仑势由经典库仑公式描述，与原子距离$r$的1次幂的倒数相关。因此它在原子距离较远时衰减速度比Lennard-Jones势能的6次幂和12次幂要慢，原子距离较远时库仑力要大于范德华力；而当原子距离靠近时，12次幂的斥力势能增长极快，因此表现出完全由范德华力贡献的斥力。

库仑势有四个参数，介电常数参数项$1/{4\pi\epsilon_0}$是常数，为$332.0636 kcal \cdot \text{\AA}/(mol \cdot e^2)$或$138.935458 kJ \cdot nm/(mol \cdot e^2)$，相对介电常数$\epsilon_r$在无外加反应场的显式水体系或真空体系下为1，两个原子的电荷参数$q$的单位为$e$。

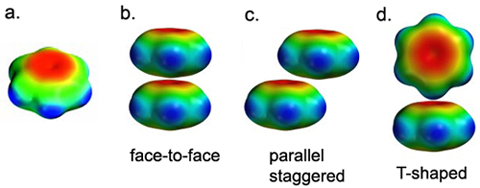
图1.2 π-π堆叠的静电势模型

除了描述正负电荷之间的相互作用外，分子中原子的偏电荷(partial charge)通过规则性的分布可以描述特殊的相互作用，如π-π堆叠。π-π堆叠的本质是色散作用，分子力场中是没有专门描述色散作用的参数的，是通过原子的偏电荷来描述的。比如苯环的C一般带有部分的负电荷，苯环的H一般带有部分的正电荷，因此当苯环处在T-shape时，正电荷的H会处在负电荷的C环的中心，从而降低库仑势；苯环处在错位平行时，两个苯环的正电荷的H位于负电荷的C环的中心，也能降低库仑势。苯环处在面对面平行时则略有不同，库仑势其实是互斥的，此时的整体力场能量降低是通过范德华势主导的。

氢键项

早在AMBER94/96时代，AMBER力场中包含了一个氢键项。早期的AMBER力场使用类似用12-10的类Lennard-Jones势能函数进行描述：

$$\tag{1.8} v_{hbonds}=(\frac{A_{ij}}{r_{ij}})^{12}-(\frac{C_{ij}}{r_{ij}})^{10}$$

实际上由于氢键本质主要就是静电作用，使用H原子和氢键受体原子的电荷带来的库仑作用表现就能够描述得比较理想，因此目前主流力场大多没有氢键项，12-10函数目前已经不再流行。

成键项

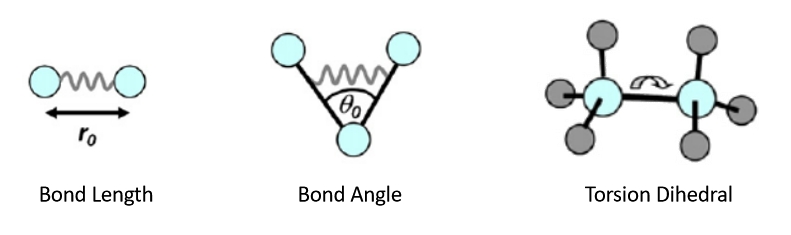
图1.4 成键项中的键长，键角和二面角的相应运动模式

键长-键伸缩能

键伸缩能描述两个成键原子之间的关系。形成化学键的原子之间会在平衡长度附近振荡，靠近时原子间产生强大的斥力，远离时引力下降能量上升直到原子间不再有相互作用，即键的断裂。这一能量曲线可以以Morse曲线进行描述。但在分子动力学模拟中，原子之间不会发生键的断裂（如果需要考虑键的断裂，可以使用QM/MM模拟），因此我们只需要考虑成键距离附近的振荡，即通过简单的简谐项对成键项进行描述:

$$\tag{1.9} v(l) = \frac{k_{l_i}}{2} (l_i-l_{i,0})^2$$

平衡位置时键伸缩项能量最低。

单一简谐项足够描述大部分成键项，如果想要更精确描述成键项，我们也可以增加二阶、三阶、甚至更高阶的简谐项。比如：

$$\tag{1.10} v(l) = \frac{k_{l_i}}{2} (l_i-l_{i,0})^2[1-k'(l-l_0)-k''(l-l_0)^2-k'''(l-l_0)^3...]$$

高阶简谐项虽然提高精度，但带来了巨大的计算量提升，因此我们实际使用的AMBER力场只使用了一阶简谐项。

简谐项中存在两个参数：$k_{l_i}$，键的平衡常数，单位为$kcal/(mol \cdot \text{\AA}^2)$或$kJ/(mol \cdot nm^2)$；键的平衡距离$l_0$，单位为$\text{\AA}$或$nm$。比如GAFF中乙烷的C-C键的平衡常数为$303.1kcal/(mol \cdot \text{\AA}^2)$，平衡距离为为$1.535\text{\AA}$

键角-键弯曲能

键弯曲描述键角的张合，是成键的三个原子之间的关系。与键伸缩运动类似，键角的弯曲也发生在平衡角附近振荡，因此AMBER力场使用了简谐项对键角进行描述：

$$\tag{1.11} v(\theta) = \frac{k_{\theta_i}}{2} (\theta_i-\theta_{i,0})^2$$

平衡位置时键弯曲项能量最低。

同样，也可以使用高阶项提高准确度，但更高的计算量使这一选项没有实际价值，因此AMBER力场中也只使用一阶简谐项。

$$\tag{1.12} v(\theta) = \frac{k_{\theta_i}}{2} (\theta_i-\theta_{i,0})^2[1-k'(\theta-\theta_0)-k''(\theta-\theta_0)^2-k'''(\theta-\theta_0)^3...]$$

其中$k_{\theta_i}$为键角的平衡常数，单位为$kcal/(mol \cdot Degree^2)$或$kJ/(mol \cdot Degree^2)$；键的平衡距离$\theta_0$，单位为$Degree$。比如GAFF中，TIP3P水分子的H-O-H的平衡常数为$43.276 kcal/(mol \cdot Degree^2)$，平衡角度$104.52\degree$，夹角小于$109\degree$，符合孤对电子对H-O-H键角挤压的化学经验。甲烷的H-C-H的平衡常数为$38.802 kcal/(mol \cdot Degree^2)$，平衡角度$108.46\degree$，即标准的$109\degree$正四面体结构时的键角。

二面角-键扭转能

键扭转的能量描述四个成键原子间的关系，即四个原子间构成的二面角与能量的函数曲线。这里我们不能再以简谐项描述二面角的扭转，除少量的阻转二面角或双键、芳香键的二面角几乎处在平衡位置，可以使用简谐项外，大部分二面角是可以360°旋转的。比如乙烷的二面角进行能量扫描后的势能曲线，在0°，120°，240°时为重叠式，能量最高；60°，180°，300°时为交错式，能量最低。

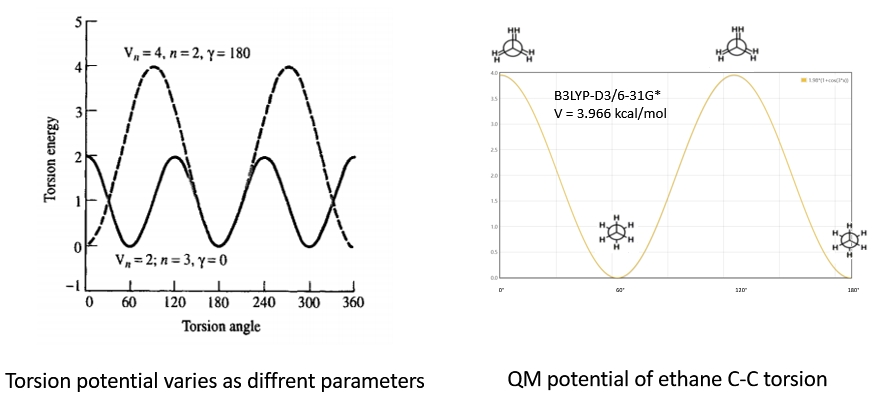
图1.5 不同参数下二面角的键扭转能和乙烷的C-C键扭转能

描述此类周期性变化的函数一般选择傅里叶级数，即多个三角函数的组合。不同力场使用的函数形式不同，但仍然可以按照周期大致分类为周期函数类型，简谐势类型和表格势类型。周期函数类型的二面角函数为最主要的二面角，比如AMBER，CHARM，OPLS中都以此类函数为主；简谐函数的二面角函数，也叫二次幂二面角（Quadratic Dihedral），使用力场较少；表格势（Tabular Dihedral）则通常用于描述氨基酸残基的Rotamer，如AMBER和CHARMM力场中的CMAP函数。

周期函数类型：

$$\tag{1.13} v(\omega)=\displaystyle\sum_{n=0}^NC_n\cos(\omega)^n \\ v(\omega) = \displaystyle\sum_{n=0}^N \frac{V_n}{2}[1+\cos(n\omega-\gamma)]$$

简谐函数类型：

$$\tag{1.14} v(\omega)=K_d(\omega-\omega_0)^2$$

表格势类型

index	angle	energy	derivative
$i_1$	$a_1$	$e_1$	$de_1$
-------	-------	-------	--------
$i_N$	$a_N$	$e_N$	$de_N$

AMBER力场中使用的是周期函数类型：

$$\tag{1.15} v(\omega) = \displaystyle\sum_{n=0}^N \frac{V_n}{2}[1+\cos(n\omega-\gamma)]$$

其中$N$代表的是该二面角由几个周期函数组合而成，对于GAFF力场，大部分二面角的N=1，如乙烷的二面角，又如双氮甲烷Azomethane的两个SP2杂化的N之间的键的二面角则用两个函数组合，N=2。

AMBER力场的二面角函数形势中有3个参数，$V_n$为势垒能（单位为$kcal$或$kJ$），$n$为周期，$\gamma$为相位（单位为$Degree$）。

甲烷的H-C-C-H二面角：

$$\tag{1.16} v(\omega) = 0.15 \times [1+\cos(3 \times \omega-0.0)]$$

可以基本上定量准确地描述乙烷的旋转，在0°，120°，240°时为重叠式，能量最高；60°，180°，300°时为交错式，能量最低。由于乙烷有9个H-C-C-H二面角，因此实际上的能垒还要乘以9，所以能垒最高为2.70 kcal/mol。但是相比量化扫描的势能面，仍然低1.27 kcal/mol，原因将在后文揭晓。

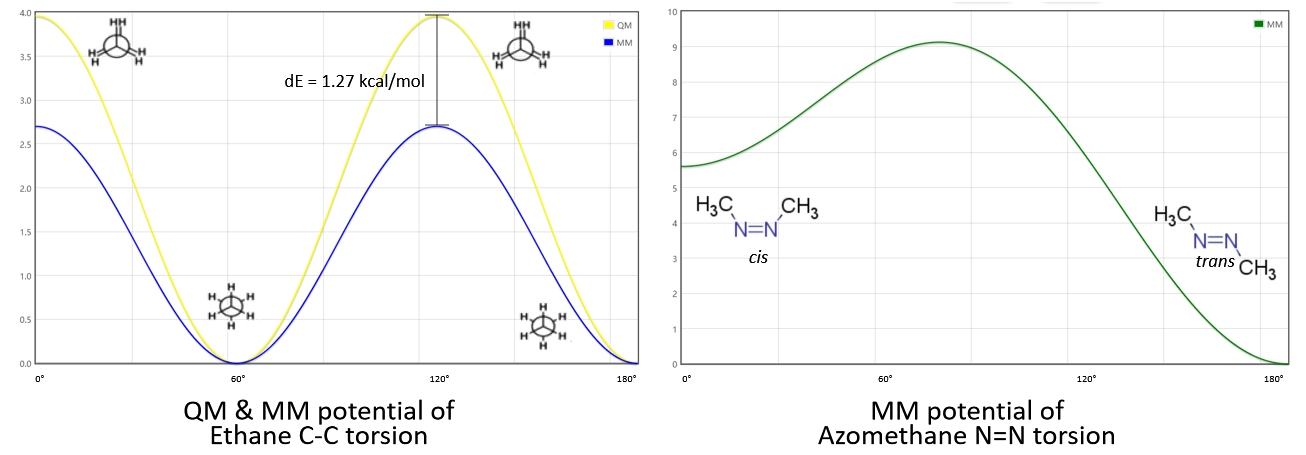
图1.6 量化和力场计算的乙烷的C-C键扭转能和双氮甲烷N=N键扭转能

双氮甲烷Azomethane的C-N=N-C二面角：

$$\tag{1.17} v(\omega) = 3.0 \times [1+\cos(2 \times \omega-180.0) ]+ 2.8 \times [1+\cos(1 \times \omega-0.0)]$$

可以定性地描述双氮甲烷的二面角，即不可旋转，顺势能量高于反式能量，但能垒准确度仍与量化扫描势能面存在差距。

异二面角

对于苯环上的氢或碳，环丁酮的氧，如果我们只使用常规的二面角模型描述所有的旋转键项，这些原子是无法维持结构的平面性的，因此力场中定义了异二面角(Improper Dihedral)参数。

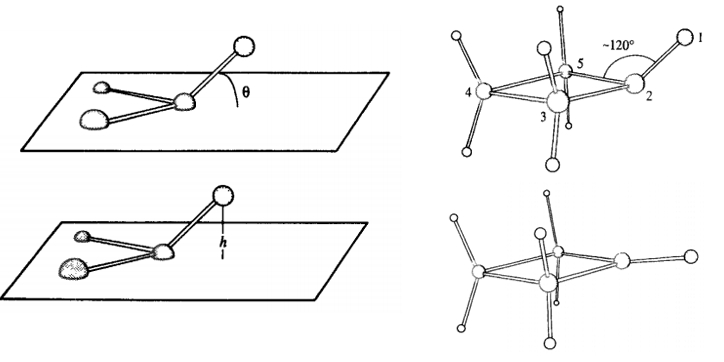
图1.7 异二面参数维持平面或平面外原子的平面性

异二面角完全可以通过简谐势描述，即：

$$\tag{1.18} v(\theta) = \frac{k}{2}\theta^2$$

$$\tag{1.19} v(\theta) = \frac{k}{2}h^2$$

一种是以原子偏离平面的角度作为变量，另一种是以原子偏离平面的高度作为变量。

$$\tag{1.20} v(\omega) = \displaystyle\sum_{n=0}^N \frac{V_n}{2}[1+\cos(n\omega-\gamma)]$$

另一种方式则仍然使用二面角函数，将二面角定义为环上的三个原子和另一个环外的原子之间的关系，相位为180°，即平面时能量最低。AMBER使用的就是这种形势。使用这种函数形势的好处是不要再新增一个计算四原子关系的简谐势函数，借用常规二面角函数形势就可以，减少了计算量。

因为维持平面所需的能量并不高，因此大部分情况下如GAFF使用1.1 kcal/mol的能垒就可以维持苯环的取代基团的平面性，只有极少(2个)特例会使用10.5 kcal/mol维持平面性。

1,4-相互作用

在二面角一节中，我们发现乙烷的C-C键在旋转时的能垒比量化扫描的势能曲线低，这是因为缺少了力场中的1,4-相互作用。

除去成键项外，还有并不直接相连成键原子之间的非键相互作用，比如键弯曲的第1,3号原子间的相互作用，键旋转的1,4号原子间的相互作用。如果两个原子是成键原子，那么他们之间的库仑力和范德华力都会非常大，这是不合理的，所以没有1，2之间的非键项。同理，1，3原子间的非键项也不需要考虑。从另一角度也可以解释，键伸缩的力场数一般在百kcal/mol左右，键弯曲的力场数在几十kcal/mol左，因此非键项中的范德华和库仑力相比成键项基本可忽略不计。

但是对1,4原子则不同，1,4原子之间是存在非键相互左右的，二面角函数是无法完全描述两个原子之间的相互作用，1，4原子之间的非键项是不完全的，AMBER力场中会对1，4原子之间的范德华项和库仑项分别乘以一个缩放系数，即0.5倍的范德华项和0.8333的库仑项。AMBER力场中只考虑了1,4相互作用的能量缩放，对于1,5相互作用或更远的分子内原子关系都采用完全的、非缩放的范德华项和库仑项进行描述。

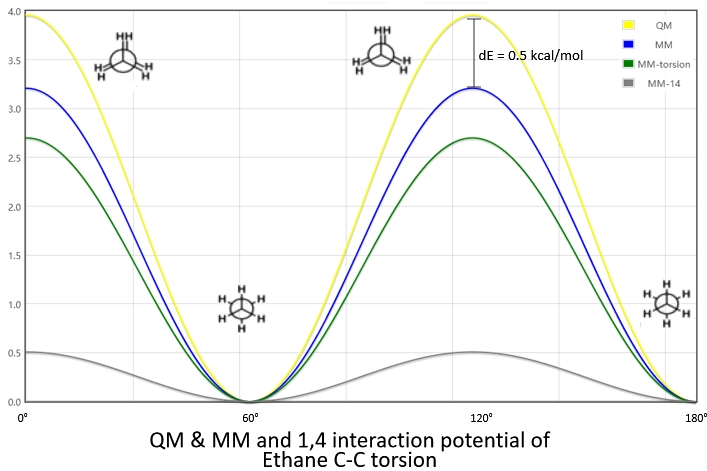
图1.8 1,4相互作用能减小二面角的误差

如果我们在乙烷的C-C键旋转势能加上缩放的非键项，就可以看到乙烷的二面角的势能曲线更接近量化扫描的势能曲线，误差从1.27 kcal/mol缩小到0.5 kcal/mol。这也说明了完整的二面角参数是由二面角函数和1,4作用能加和构成的。在GAFF这类通用小分子力场中，这样做的好处是即便二面角函数的参数一致，通过1,4作用能也可以区分大部分变化微小的二面角。

协同项

各种成键项之间的协同项，形式复杂，拟合困难，虽然精度或许有提升，但对于动力学模拟来说十分鸡肋。比如键伸缩和键弯曲的协同项，或键弯曲和键旋转的协同项。在MM系列小分子力场，以及MMFF94小分子力场中有此类参数，但AMBER和GAFF中则没有此类参数项。

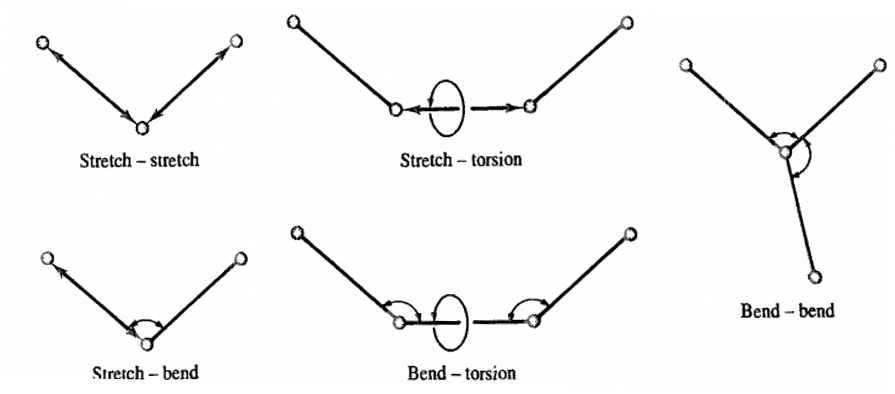
图1.9 力场中的协同项

如图1.9所示，力场中的成键项之间都可以构造协同项函数，比如MMFF94中的键长-键角协同项：

$$\tag{1.21} V_{BA}= 2.51210( k_{ba,ijk} \Delta r_{ij} + k_{ba,kji} \Delta r_{kj}) \Delta \Theta_{ijk}$$

其中$k_{ba,ijk}$和$k_{ba,ijk}$是键长-键角协同项的两个力常数，$\Delta r_{ij}$，$\Delta r_{kj}$，$\Delta \Theta_{ijk}$为两个键长和所夹键角的力常数。

因此类参数导致MMFF94的完整力场形势稍显复杂，所以大多数主流的分子模拟软件Gromacs，Amber，OpenMM，Desmond无法支持MMFF94力场的分子动力学模拟，只有Tinker支持。值得一提的是Tinker也支持复杂的可极化力场AMOEBA/AMOEMA+。

小结

本文以AMBER力场形势为主介绍了分子力场的函数形势和参数意义，读者应该在读完文章后能够熟练写出力场函数形势和重要参数的单位和意义，后续文章中将以GAFF力场文件为参考讲述具体的力场参数和力场参数的来源，为后续优化具体小分子的力场提供指导。