DeepSeek与药代动力学

Posted on

大语言模型出现后，我一直在尝试在药研工作中使用它们，比如名词解释，文献翻译和文献解释，我也在期待有更好的药研Agent诞生。今年最火的大语言模型就是DeepSeek，特别是DeepSeek-R1，思考的过程不仅仅是给用户的展示，而是真实的在模型推理中进行逻辑思考。我在最近的一份工作尝试使用DeepSeek对我们的药物的药代动力学进行描述，来评价该药物是否已经有足够的活性。对于DeepSeek-V3，我需要反复修正问题并指出错误，而DeepSeek-R1几乎仅靠自己就完成了思考和错误修正。

DeepSeek

打开DeepSeek的官网，在对话框中输入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
你是一个药物研发专家，精通药化，药理和生物学基础知识，精通Python科学计算，你将回答专业药物研发问题，协助提问者优化靶点化合物活性，化合物结构，化合物ADMET性质。
你需要根据以下三个单引号中的药物PK属性和具体要求，使用Python（标准包外只使用numpy, scipy, matlotlib）绘制药代动力学曲线曲线，并保存图片。

'''
一个PROTAC分子，分子量800. 
假设该分子口服PO给药后24小时内测得PK数据中, 血药浓度是: 0h~0ng/ml, 0.25h~800ng/ml, 0.5h~1600ng/ml, 1h~900ng/mol, 2h~400ng/ml, 4h~200ng/ml, 8h~100ng/ml, 24h~0.0ng/ml。
实验测得的药物的脑/血浆药物浓度比值为0.02, 即脑内药物浓度是血药浓度2%。
该药物实测的靶点降解DC50浓度是8nM（nmol/L）。
假设靶点的最大恢复速度是2.8%/h。
缺失参数请使用药理模型中的通用公式进行补充并给出解释：如靶点的降解速率应该与DC50有关，注意靶点的含量上下界在0%-100%。

**每一步计算需给出数学公式进行解析**

最后：计算48h内的QD(24h给药一次), BID(24h给药两次)给药条件下的药物浓度曲线和靶点浓度曲线，药物浓度使用次坐标轴, 靶点百分比使用主坐标轴。血药浓度PK曲线是实测值，因此在采样点之间通过线性插值来填充缺失数据，不要拟合。'''

Python代码写在推理最后部分。

DeepSeek-R1思考了8分钟(471s，~11000 Tokens)，给出了如下思考

嗯，我需要帮助用户解决一个关于药代动力学和药效动力学的问题。首先，用户希望根据提供的PK数据绘制药代动力学曲线，并计算两种给药方案下的药物浓度和靶点浓度变化。同时，用户还提到需要处理脑浓度、DC50以及靶点恢复速率等参数。让我仔细分析一下问题。

首先，用户给定了口服给药后的血药浓度数据，时间点从0到24小时，对应的浓度值。需要根据这些数据用线性插值生成连续的浓度曲线，而不是拟合模型。这可能意味着在Python中使用插值方法，比如线性插值，来填充时间点之间的浓度值。

接下来，用户提到脑/血浆浓度比是0.02，所以脑内的浓度应该是血浆浓度的2%。这部分比较简单，直接对每个时间点的血药浓度乘以0.02即可得到脑浓度。但需要注意单位是否一致，给出的数据中血药浓度是ng/ml，而DC50是8nM，可能需要单位转换。

然后是关于靶点降解的部分。已知DC50是8nM，即达到50%靶点降解所需的浓度。这里需要用药物浓度来计算靶点的降解速率，同时靶点的恢复速率是2.8%/h。靶点的含量必须在0%到100%之间。这里可能需要使用微分方程来描述靶点浓度的变化，即降解和恢复的动态平衡。

用户提到缺失的参数需要用通用药理模型补充，并给出数学公式。例如，靶点的降解速率可能与DC50有关。可能需要使用Hill方程之类的公式，比如靶点降解速率= (Cn)/(Cn + DC50^n) * k_degradation，其中n是Hill系数，假设为1的情况下简化为C/(C + DC50)。不过这里可能需要更具体的模型。例如，靶点的降解可能遵循dE/dt = k_degradation * (C/(C + DC50)) * (1 - E) - k_recovery * E，其中E是靶点的被降解比例，或者类似的形式。或者，可能靶点的浓度变化由两部分组成：药物导致的降解和自然恢复。例如，dE/dt = (E_max * C)/(EC50 + C) - k_recovery * E，其中E_max是最大效应，这里可能E_max对应100%降解，但需要确认模型结构。

另外，用户要求计算48小时内QD和BID给药条件下的情况。QD是每24小时给药一次，BID是每12小时给药两次，总共两次给药。每次给药后的血药浓度曲线需要叠加。这里可能需要考虑药物在多次给药后的累积情况，但由于用户说明PK曲线是实测的，并且使用线性插值，所以可能需要将每次给药后的浓度曲线叠加起来。例如，在BID情况下，第二次给药在24小时后的12小时，即第12小时给药，那么总的48小时里会有两次给药：0小时和12小时？或者原题中的BID是24小时两次，可能间隔12小时？需要明确给药时间。原题中说BID是24h给药两次，可能每12小时一次，比如在0小时和12小时给药，然后第二个给药在24小时？可能用户的意思是BID是每12小时一次，所以在48小时内，QD是两次给药（0h和24h），BID是四次给药（0h,12h,24h,36h）？需要确认。或者原题中“24h给药两次”可能是指在24小时内给药两次，即每12小时一次。例如，在0和12小时给药，之后在24小时再给药吗？可能用户的意思是，对于BID给药，每次给药间隔12小时，所以在48小时内，总共有四次给药：0、12、24、36小时。但需要根据问题描述中的具体说明。原题中的描述是“BID(24h给药两次)”，可能指在24小时内给药两次，即两次间隔12小时。所以对于48小时的总时间，QD是每24小时一次（0和24小时），而BID是每12小时给药，在0、12、24、36小时给药。因此，在计算浓度时，需要将每次给药后的浓度曲线进行叠加。

接下来，如何叠加多次给药的浓度曲线？例如，每个给药后的浓度曲线是根据单次给药的PK数据，通过时间平移相加。例如，第一次给药在0小时，得到的浓度曲线是C(t)；第二次在12小时，浓度曲线是C(t-12)叠加到总浓度上。但需要注意，如果PK数据是单次给药的实测数据，那么多次给药的浓度是各次给药后的浓度之和？或者是否考虑药物的吸收、分布、代谢等因素导致的非线性叠加？不过用户要求使用实测数据，并在采样点之间线性插值，所以可能需要将每次给药后的浓度曲线按照时间叠加。例如，对于BID给药，每次给药后的血药浓度随时间变化的曲线是单次给药的曲线，但每次给药后的时间点会叠加到总的时间轴上，然后总浓度是各次给药后的浓度在该时间点的总和。这可能需要进行卷积或者直接叠加。

但这里可能有一个问题：当多次给药时，药物是否在体内线性叠加？例如，假设药物的PK曲线在每次给药后独立，那么总浓度是各次给药后的浓度曲线的叠加。这可能适用于线性药代动力学的情况，而用户是否假设这种情况呢？根据用户的要求，可能需要这样处理，因为用户没有提到其他复杂的药动学模型，如非线性消除等，所以可能可以假设线性叠加。

所以，处理多次给药的方式是，对于每个给药时间点，生成单次给药的浓度曲线，然后将所有曲线在时间轴上叠加，得到总浓度。例如，对于QD给药，第一次在0小时，第二次在24小时。第一次给药的浓度持续到24小时，而第二次给药后的浓度从24小时到48小时。但原题的PK数据是在给药后24小时浓度回到0。所以单次给药后，浓度在24小时时为0。因此，在QD情况下，第二次给药在24小时时，此时第一次给药的浓度已经为0，所以两次给药的浓度不会叠加。而BID情况下，给药间隔12小时，比如在0、12、24、36小时给药，那么每次给药后的浓度曲线会叠加。例如，在12小时给药后，其浓度曲线在12到36小时之间，此时第一次给药的浓度在12小时已经下降到某个值，需要将两者相加。

但根据用户给出的单次给药后的浓度数据，在24小时时血药浓度为0。因此，单次给药后的作用时间到24小时。因此，如果第二次给药在12小时，那么第一次给药的浓度在12小时时的浓度是？原数据中的时间点是0.25h、0.5h等，但在12小时时，原数据中的浓度是根据线性插值得出的。原数据中的时间点最大到24小时，所以当给药在0小时时，在0到24小时之间的浓度由线性插值得到。当第二次给药在12小时时，该次给药的浓度曲线会覆盖12到36小时，但根据原数据，单次给药后24小时浓度是0，所以第二次给药在12小时后，其浓度在12+24=36小时时为0。因此，在BID给药的情况下，每个给药后的浓度曲线持续24小时，因此每次给药后的浓度在各自的时间段内存在，并且可能在时间重叠部分相加。

例如，第一次给药在0小时，其浓度在0-24小时之间，根据插值的数据。第二次给药在12小时，其浓度在12-36小时之间。所以在12-24小时之间，两次给药的浓度相加。第三次给药在24小时，浓度在24-48小时之间。第四次给药在36小时，浓度在36-60小时，但用户需要的是48小时内的数据，所以可能第四次给药在36小时，其浓度到48小时时还未归零，需要计算到48小时。不过原题中的BID给药是“24h给药两次”，即可能在24小时内给药两次，例如每12小时一次。所以在48小时内，总共有4次给药（0,12,24,36小时）。此时，每次给药的浓度曲线相互叠加。比如，在时间点t=12小时，第一次给药的浓度是经过12小时后的值，而第二次给药后的时间点为0小时，所以此时第二次给药的浓度是0，直到0.25小时后开始上升。这时候可能需要将每次给药的浓度曲线在时间轴上对应的时间点相加。

因此，处理多次给药的步骤可能是：

  1. 对于每个给药时间点（比如0、12、24、36小时），生成该次给药后的时间-浓度曲线，覆盖给药后的0到24小时的时间段。

  2. 将这些曲线在总的时间轴（0到48小时）上叠加，即每个时间点t的总浓度是各次给药在t时刻的浓度之和。

例如，在时间t=12小时，第一次给药后的浓度是给药后12小时的浓度值，而第二次给药后的浓度是给药后的0小时，即0浓度。在时间t=13小时，第一次给药的浓度是给药后13小时的浓度（根据插值数据），而第二次给药的浓度是给药后的1小时浓度（900 ng/ml），所以总浓度是两者相加。

现在需要将这些步骤转化为Python代码。首先，处理单次给药的浓度曲线，使用线性插值。然后，对于多次给药，生成各次给药的浓度时间序列，并将它们叠加。

接下来，关于靶点浓度的计算。用户要求根据药物浓度计算靶点的百分比变化。假设靶点的降解速率与药物浓度有关，并且靶点自身有恢复速率。这里可能需要建立微分方程模型。

例如，假设靶点的浓度（未被降解的比例）为E(t)，其变化率由两部分组成：药物导致的降解和自然恢复。假设药物存在时，导致靶点的降解，而自然恢复则使靶点浓度回到基线。例如，dE/dt = k_recovery * (1 - E) - k_degradation * (C(t)/ (C(t) + DC50)) * E，或者类似的公式。或者，可能靶点的降解速度与药物浓度相关，而恢复速度是恒定的。

用户提到“靶点的最大恢复速度是2.8%/h”，这可能意味着恢复速率是2.8%每小时。例如，当药物不存在时，靶点浓度会以2.8%每小时的速度恢复。例如，dE/dt = 2.8% * (1 - E)，如果E是当前靶点的剩余浓度百分比。或者，假设当没有药物时，靶点的恢复速率是2.8%每小时，即 dE/dt = 0.028 * (1 - E)。而当药物存在时，降解速率可能由药物浓度决定。

另外，DC50是8nM，所以当药物浓度等于DC50时，降解速率可能达到最大的一半。这里可能需要使用类似于Hill方程的模型，如降解速率 = (C(t)n)/(DC50n + C(t)^n)。假设n=1的情况下，可以简化为 C/(C + DC50)。然后，最大降解速率可能取决于药物浓度，当药物浓度很高时，降解速率趋近于某个最大值。但用户给出的参数中没有提到最大降解速率，可能需要假设降解速率是与药物浓度相关的一个比例因子，乘以某个最大降解速率常数。或者，可能靶点的降解速率与药物浓度的关系是：当药物浓度存在时，靶点的降解速率与药物浓度和靶点当前浓度的乘积有关，而恢复速率是固定的。

例如，可能采用如下模型：

dE/dt = k_degradation * (C(t)/(C(t) + DC50)) * (1 - E) - k_recovery * E

其中，E是靶点的被降解的百分比（即假设E是降解的比例，所以未被降解的比例是1-E？或者E是剩余的靶点浓度百分比？需要明确模型的变量定义。例如，如果E是剩余靶点浓度的百分比（0-100%），那么降解会导致E减少，恢复导致E增加。或者可能相反。或者，假设当药物存在时，靶点被降解，导致E下降，而当药物不存在时，E逐渐恢复。

比如，当药物浓度高时，靶点的降解速度加快，导致E降低，而恢复速度使E增加。可能需要更具体的动力学模型。例如，假设：

dE/dt = - (k_max_degradation * C(t)) / (C(t) + DC50) * E + k_recovery * (1 - E)

其中，k_max_degradation是最大降解速率常数，k_recovery是恢复速率常数。在这种情况下，当药物浓度足够高时，降解速率趋近于k_max_degradation，导致E的减少，而恢复项则使E趋向于1（即100%的靶点浓度）。

不过用户给出的参数中只有靶点的最大恢复速度是2.8%/h，这应该对应k_recovery=0.028 /h。而降解速率可能与DC50有关。例如，当药物浓度等于DC50时，降解速率是最大降解速率的一半。但用户没有提供最大降解速率，可能需要假设。或者，是否降解速率与药物浓度成正比？例如，当药物浓度为C时，降解速率为 (C / DC50) * k，当C << DC50时，速率很低，当C = DC50时，速率为k，当C >> DC50时，速率可能超过k？或者使用类似米氏方程的形式。

这里可能需要做一些假设。例如，假设靶点的降解速率与药物浓度和当前靶点浓度的乘积有关，同时受DC50的影响。例如：

降解速率 = (C(t) / DC50) * (1 - E(t))

而恢复速率是0.028 * E(t)（假设当没有药物时，E会以2.8%每小时恢复）。或者，恢复速率可能和剩余的靶点量有关，比如恢复速率是0.028*(1 - E(t))。

或者，可能更合理的模型是：当药物存在时，靶点的降解速率与药物浓度和靶点当前浓度的乘积成正比，并且受DC50的影响。例如：

dE/dt = - ( (C(t) / DC50) / (1 + C(t)/DC50 )) * E(t) + k_recovery * (1 - E(t))

这里，当药物浓度很高时，降解速率趋近于 E(t) 的减少速率的最大值。但可能需要调整模型参数。或者，假设药物引起的降解速率与药物浓度和靶点浓度的乘积成比例，而恢复速率与（1 - E）成比例。例如：

dE/dt = -k_degradation * (C(t)/(C(t) + DC50)) * E + k_recovery * (1 - E)

这里，k_degradation是最大降解速率常数。但用户没有给出这个参数，可能需要假设。或者，用户提到的“靶点的降解速率应该与DC50有关”，可能需要根据DC50推导出降解速率常数。例如，可能假设当药物浓度等于DC50时，降解速率等于恢复速率，以达到稳态？或者需要其他方式确定参数。

这个问题可能需要进一步的假设。例如，假设当药物浓度在DC50时，降解速率等于恢复速率，从而在稳态时靶点浓度保持平衡。这可能是一个合理的假设，因为DC50是导致50%靶点降解的浓度。例如，当药物浓度等于DC50时，降解速率等于恢复速率，此时靶点浓度处于平衡状态。

假设当C=DC50时，降解速率等于恢复速率：

k_degradation * (C/(C + DC50)) * E = k_recovery * (1 - E)

当C=DC50时，代入得到：

k_degradation * (DC50/(DC50 + DC50)) * E = k_recovery*(1 - E)

即：

k_degradation * 0.5 * E = k_recovery*(1 - E)

此时，假设在稳态下，E的值为某个值，比如当C=DC50时，靶点的降解达到50%（即E=50%），那么代入上式：

k_degradation * 0.5 * 0.5 = k_recovery*(1 - 0.5)

即左边为0.25 k_degradation，右边为0.5 k_recovery。等式变为0.25k_degradation = 0.5k_recovery → k_degradation = 2 k_recovery

而k_recovery已知是0.028 /h（因为最大恢复速度是2.8%/h，即每小时恢复2.8%的靶点，这可能对应于恢复速率k_recovery=0.028 /h）。因此，k_degradation = 2 * 0.028 = 0.056 /h。

这可能是一个合理的假设，即当药物浓度等于DC50时，降解速率等于恢复速率，使得在稳态时靶点浓度为50%。因此，此时靶点的降解速率常数为0.056 /h。

综上，靶点浓度的微分方程可以写成：

dE/dt = - (0.056 * (C(t)/(C(t) + DC50)) ) * E + 0.028 * (1 - E)

其中，E是靶点当前的浓度百分比（0到1之间），C(t)是药物浓度。当药物浓度高时，降解项占主导，导致E减少；当药物浓度低时，恢复项占主导，E增加。

现在需要将药物浓度转换为摩尔浓度，因为DC50的单位是nM。用户提供的血药浓度数据是ng/ml，需要将其转换为nM。药物的分子量是800 g/mol，即800 Da。

转换公式为：浓度（nM）= (浓度 ng/ml) * (1e-9 g/ng) / (分子量 g/mol) * 1e9 nmol/mol → 简化后为 (浓度 ng/ml) / (分子量) * 1e3 → 因为 1 ng/ml = 1e-9 g/L，除以分子量（g/mol）得到 mol/L，即 M，再乘以1e9得到 nM。

例如，浓度ng/ml为800 ng/ml，转换为nM：

(800 ng/ml) * (1 g / 1e9 ng) / (800 g/mol) * 1e9 nmol/L → 800/(800) * 1e9/1e9 = 1 nM。哦，等一下，这似乎有问题。正确的转换步骤应该是：

浓度（nM）= (浓度 ng/ml) * (1e-6 g/L) / (分子量 g/mol) * 1e9 nmol/mol

因为 1 ng/ml = 1e-6 g/L。例如：

浓度（nM）= (浓度_ng_per_ml) * 1e-6 g/L / (MW g/mol) * 1e9 nmol/L

= (浓度_ng_per_ml * 1e-6) / (MW) * 1e9

= 浓度_ng_per_ml * (1e3 / MW )

例如，当MW=800时：

nM = 浓度_ng_per_ml * 1000 / 800 = 浓度_ng_per_ml * 1.25

所以，800 ng/ml的血药浓度转换为800 *1.25 = 1000 nM。而DC50是8nM，这意味着在800ng/ml的血药浓度下，药物浓度是1000nM，远远超过DC50，所以此时降解速率会很高，导致靶点浓度迅速下降。

但用户给出的数据中的血药浓度是血浆中的浓度，而药物在脑中的浓度是2%的血浆浓度。所以是否需要将脑中的浓度用于靶点降解？或者问题中的靶点是否位于中枢神经系统，需要脑浓度？或者假设靶点降解主要受血浆浓度影响？这里可能需要明确。根据问题描述，用户给出的脑/血浆比值是0.02，但药物的靶点降解DC50是8nM，这可能指的是体外测得的浓度，或者体内有效浓度。可能假设靶点位于体内，所以药物在作用部位的浓度是血浆浓度或者组织浓度？或者可能此处的DC8nM是基于体外实验，而体内效应需要考虑药物的分布。例如，假设药物在靶组织中的浓度等于血浆浓度，或者等于脑中的浓度？这点需要用户澄清，但根据问题描述，可能用户希望将血浆中的浓度用于计算靶点降解，或者可能将脑中的浓度作为有效浓度？这可能是一个关键点，因为如果靶点位于脑部，则使用脑浓度；否则使用血浆浓度。用户的问题描述中没有明确说明，但给出的脑浓度比值可能是一个额外信息，但可能不影响靶点降解的计算，因为DC50是体外测得的。需要用户澄清，但此处可能假设靶点的有效浓度是血浆中的浓度，即药物在作用部位的浓度等于血浆中的浓度，或者是否需要考虑分布？可能根据问题要求，用户可能希望将血浆浓度作为有效浓度，因此将血浆中的浓度转换为nM后，用于计算靶点降解。

或者，可能药物需要进入脑组织才能发挥作用，此时DC50是基于脑内的浓度？但问题中的描述并没有明确这一点。这里可能需要进一步假设。例如，如果PROTAC分子作用于中枢神经系统外的靶点，那么血浆浓度是有效的；如果靶点位于脑内，则脑浓度是有效的。假设问题中的靶点位于脑外，因此使用血浆浓度转换为nM后的值来计算靶点降解。或者用户可能希望考虑脑浓度，所以需要将血浆浓度乘以0.02得到脑浓度，再转换为nM。这里可能需要用户澄清，但问题中的描述提到“脑/血浆药物浓度比值为0.02”，即脑内浓度是血浆浓度的2%。而DC50是8nM，所以可能需要将脑内的浓度与DC50比较，或者是否该PROTAC的靶点在脑内，所以需要脑内的浓度？

这会影响最终的靶点降解曲线。例如，假设靶点位于脑内，则有效浓度是脑内的浓度（血浆浓度的2%）；否则，有效浓度是血浆浓度。例如，如果PROTAC的靶点位于脑外，则有效浓度是血浆中的浓度。此时，需要明确问题中的靶点是否位于脑部。由于用户没有说明，可能需要假设有效浓度是血浆浓度，或者在问题处理中，可能需要同时考虑两种情况。但根据问题中的描述，可能用户希望将脑浓度作为有效浓度，因为DC50可能是在体外测得的，而体内需要达到相应的浓度才能有效。例如，如果药物在血浆中的浓度很高，但进入脑部的浓度较低，可能无法有效降解脑内的靶点。但问题中的DC50是8nM，可能是指体外实验中的浓度，而体内的有效浓度可能需要达到该浓度在作用部位。因此，可能需要根据问题中的具体数据来进行判断。这里可能需要用户澄清，但根据问题描述，可能需要使用血浆中的药物浓度来计算靶点降解，因为脑中的浓度可能不足以达到DC50。例如，原题中的DC50是8nM，而血浆中的浓度在最高点是1600 ng/ml，转换为nM是1600 * 1.25 =2000 nM，远远超过8nM。但脑中的浓度是2%的血浆浓度，即2000nM *0.02=40nM，仍然超过DC50。所以在脑中的浓度可能足够引起降解。此时，可能需要明确是否将脑中的浓度作为有效浓度，或者是否假设靶点位于全身，使用血浆浓度。例如，如果该PROTAC分子用于治疗中枢神经系统外的疾病，那么血浆浓度是有效浓度；如果用于脑部疾病，则脑浓度是有效浓度。

这里可能存在歧义，但根据问题描述，用户给出的脑/血浆浓度比值可能仅作为参考，而问题中的靶点降解可能基于血浆中的药物浓度。或者用户可能希望考虑脑浓度，但需要明确。根据问题中的要求，需要计算药物浓度曲线和靶点浓度曲线。可能这里的靶点降解基于药物的有效浓度，即血浆中的浓度。或者可能用户希望将脑浓度作为有效浓度，这可能影响计算。假设问题中的靶点降解是基于血浆中的药物浓度，那么转换后的血浆浓度将用于计算靶点降解。但需要确认这一点。

现在，假设有效浓度是血浆中的药物浓度，并将其转换为nM。例如，在0.25小时的血浆浓度是800ng/ml，转换为800 *1.25=1000nM，远高于DC50的8nM，此时降解速率将很高，导致靶点浓度迅速下降。而随着时间的推移，血浆浓度下降，降解速率降低，靶点浓度恢复。

现在，处理这些步骤：

  1. 使用Python绘制PK曲线，使用线性插值填充数据点之间的浓度。使用numpy、scipy、matplotlib。需要将给定的时间点和浓度数据存储，生成一个插值函数，然后在所需的时间点进行插值。

  2. 处理多次给药的情况，将各次给药的浓度曲线叠加。

  3. 将浓度转换为nM。

  4. 建立微分方程模型，计算靶点浓度的变化。

  5. 将药物浓度和靶点浓度绘制在同一图中，药物浓度使用次坐标轴，靶点百分比使用主坐标轴。

现在，具体步骤：

首先，处理PK数据。给定的时间点和浓度数据：

时间点：0, 0.25, 0.5, 1, 2,4,8,24小时

浓度：0, 800, 1600, 900,400,200,100,0 ng/ml

需要创建一个插值函数，在时间点之间进行线性插值。例如，在0到0.25小时之间，浓度从0线性增长到800ng/ml。在0.25到0.5小时之间，线性增长到1600，等等。在Python中，可以使用scipy的interp1d函数，设置kind=‘linear’，并假设在时间点之外的地方，浓度保持为0？或者，根据给定的数据，在24小时后浓度为0。所以对于单次给药，时间范围是0到24小时，之后浓度归零。在多次给药的情况下，每次给药的浓度曲线持续24小时，之后归零。因此，对于每次给药，在给药后的时间t，如果t <=24小时，则使用插值函数得到浓度，否则为0。

因此，在Python中，可以定义一个函数，给定给药后的时间t_post_dose（范围0到24），返回对应的浓度值，否则返回0。这样，对于每次给药，在总时间t，计算t_post_dose = t - dose_time，如果t_post_dose在0到24之间，否则浓度是0。然后，将各次给药在该时间的浓度相加。

接下来，生成时间数组，例如从0到48小时，步长0.1小时，计算每个时间点的总浓度。

接下来，处理单位转换，将总浓度（ng/ml）转换为nM。对于每个时间点的总浓度，转换为nM，即乘以1.25（因为浓度_ng_ml * 1000 / 800 = 浓度_nM）。

然后，建立微分方程模型，计算靶点浓度E(t)的变化。使用数值积分方法，例如欧拉法或者使用scipy的odeint函数。这里需要定义一个微分方程函数，根据当前的E和药物浓度C(t)，计算dE/dt的值。然后，在每个时间步长上，积分得到E(t)。

对于微分方程的求解，需要药物浓度随时间变化的函数。因为药物浓度是离散的时间点，通过插值得到连续函数，但在数值积分时需要能够在任意时间点得到浓度值。因此，在Python中，可以先创建一个插值函数，该函数返回任意时间t的血浆浓度总和（即多次给药的叠加），转换为nM后的浓度，然后这个插值函数可以传递给微分方程求解器。

或者，可以将时间离散化，例如以固定的时间步长（如0.1小时）计算浓度数组，然后在微分方程求解时，通过查找当前时间点的浓度值来进行计算。这可能更简单，尤其是当使用欧拉法进行逐步积分时。

具体来说，可以生成一个时间数组t，然后计算每个t[i]对应的总浓度C_total[i]（已转换为nM），然后使用这些数组在求解微分方程时进行线性插值，或者在每个时间步中使用对应的C值。

例如，使用欧拉法：

初始化E[0] = 100% （假设初始时靶点浓度是100%）

然后，对于每个时间步i，计算dE/dt = -0.056*(C[i]/(C[i]+8)) * E[i] + 0.028*(1 - E[i])

然后，E[i+1] = E[i] + dE/dt * dt

这里需要将C[i]的单位转换为nM，并且确保C[i]是当前时间点的浓度。

注意，这里的微分方程是否正确需要再次确认。假设E是靶点的剩余浓度（百分比），则当药物存在时，降解项导致E减少，恢复项导致E增加。例如，当药物浓度高时，降解项占优，导致E减少；当药物浓度低时，恢复项占优，导致E增加。例如，上面的微分方程是否正确？

假设：

dE/dt = 降解项的贡献 + 恢复项的贡献

降解项：药物导致E的减少，速率与C(t)、当前E的浓度有关。例如，可能降解速率与C(t)和E成正比，因为药物需要结合靶点才能降解，所以当E高时，有更多靶点可供降解。假设降解项的速率是k_degradation * (C(t)/(C(t)+DC50)) * E

恢复项：靶点以k_recovery的速率恢复，可能恢复速率与（1 - E）成正比，因为当E较低时，恢复的空间更大。例如，恢复速率是k_recovery * (1 - E)

所以，微分方程是：

dE/dt = -k_degradation * (C/(C + DC50)) * E + k_recovery * (1 - E)

其中，k_degradation = 0.056 /h，k_recovery=0.028 /h，DC50=8 nM.

这样，当药物浓度很高（C>>DC50）时，降解项变为k_degradation * E，导致E指数下降。而当没有药物（C=0）时，降解项为0，恢复项为k_recovery*(1-E)，导致E向1恢复。

现在，开始编写Python代码的大纲：

  1. 导入必要的库：numpy, matplotlib.pyplot, scipy.interpolate.

  2. 定义原始PK数据的时间点和浓度。

  3. 创建线性插值函数，处理单次给药的PK曲线。注意在时间超过24小时后浓度归零。

  4. 定义给药方案（QD：0和24小时给药；BID：0、12、24、36小时给药？需要确认具体次数。原题中的BID是24小时内给药两次，即每12小时一次。所以总给药次数在48小时为4次？例如，0、12、24、36小时各给药一次。）

但原题描述中的BID是“24h给药两次”，可能指在24小时的时间段内给药两次，即每12小时一次。所以在48小时内，BID给药两次在0和12小时，24和36小时，总共有4次给药。而QD是每24小时一次，所以在0和24小时给药，总共有两次。

所以，对于QD，给药时间列表是[0, 24]；对于BID，给药时间列表是[0,12,24,36]。

  1. 对于每个给药时间，生成该次给药后的浓度曲线，然后叠加到总浓度中。

例如，总时间范围是0到48小时，步长0.1小时。对于每个时间点t，总浓度是各次给药在时间t的浓度之和。

  1. 单位转换：将总浓度从ng/ml转换为nM。

  2. 计算靶点浓度曲线，使用微分方程模型，初始条件为E=1（100%）。

  3. 绘制双坐标轴图，主坐标轴为靶点浓度百分比，次坐标轴为药物浓度（nM）。

现在，具体步骤的Python代码：

首先，处理单次给药的PK曲线：

给定的时间点times = [0, 0.25, 0.5,1,2,4,8,24]

浓度concs = [0,800,1600,900,400,200,100,0]

在0到24小时之间，使用线性插值。超过24小时的浓度是0。

可以使用scipy.interpolate.interp1d，设置bounds_error=False，fill_value=0.

例如：

from scipy.interpolate import interp1d

times_po = [0, 0.25, 0.5,1,2,4,8,24]

concs_po = [0,800,1600,900,400,200,100,0]

创建插值函数

interp_fn = interp1d(times_po, concs_po, kind=‘linear’, bounds_error=False, fill_value=0.0)

这样，在调用interp_fn(t)时，如果t <0或t>24，返回0。

接下来，定义给药函数：

def get_concentration(t, dose_times, interp_fn):

total_conc = 0.0

for dose_time in dose_times:

t_post_dose = t - dose_time

if t_post_dose <0 or t_post_dose >24:

continue

conc = interp_fn(t_post_dose)

total_conc += conc

return total_conc

然后，生成时间数组：

t_eval = np.linspace(0, 48, 481) # 0.1小时步长，共4801点？或者 48*10+1=481点（0到48，步长0.1）

然后，对于每个给药方案，计算总浓度：

例如，QD的dose_times = [0,24]

BID的dose_times = [0,12,24,36]

然后，对于每个t_eval中的时间点，计算总浓度。

接下来，单位转换：

分子量=800 g/mol → conc_nM = conc_ng_ml * 1000 / 800 = conc_ng_ml * 1.25

所以，总浓度转换为nM是总浓度乘以1.25。

然后，计算靶点浓度E(t)：

初始化E的数组，初始值为1（100%）。

使用欧拉法逐步计算每个时间点的E值。例如：

E = np.zeros(len(t_eval))

E[0] = 1.0 # 初始为100%

dt = t_eval[1] - t_eval[0] # 0.1小时

k_degradation = 0.056 # /h

k_recovery = 0.028 # /h

DC50 =8 # nM

for i in range(1, len(t_eval)):

C = conc_nM[i-1] # 假设conc_nM是总浓度的数组，已经计算好

计算dE/dt

dEdt = -k_degradation * (C / (C + DC50)) * E[i-1] + k_recovery * (1 - E[i-1])

E[i] = E[i-1] + dEdt * dt

确保E在0到1之间

if E[i] <0:

E[i] =0

elif E[i] >1:

E[i] =1

或者，更准确的做法是，在每次迭代时使用当前时间点的C(t)，即需要将conc_nM数组对应到每个时间点的浓度。例如，如果使用欧拉法，每次的C值应该是当前时间点的浓度，而不是前一个时间点的。或者，可能需要使用更精确的积分方法，如odeint，其中在每个时间步长中计算当前的C(t)。

这可能比较复杂，因为C(t)是一个通过叠加多次给药后的插值函数得到的值。因此，更有效的方法可能是在每个时间点t_eval[i]时，计算当前的C(t)，然后代入微分方程。

例如，在欧拉法中：

for i in range(1, len(t_eval)):

t = t_eval[i]

C = get_concentration(t, dose_times, interp_fn) * 1.25 # 转换为nM

dEdt = -k_degradation * (C/(C + DC50)) * E[i-1] + k_recovery * (1 - E[i-1])

E[i] = E[i-1] + dEdt * dt

E[i] = np.clip(E[i], 0, 1)

这样，每次计算当前时间点的C(t)，并更新E。这可能更准确，尤其是当C(t)变化较快时。但这样会增加计算量，因为每次都要计算C(t)。不过，对于48小时的时间范围和0.1小时步长，这应该是可行的。

不过，在Python中，如果先生成conc_nM数组，其中包含每个时间点的浓度，那么可以在循环中直接引用conc_nM[i]，而不必每次都计算。因此，先生成总浓度数组，然后处理E。

例如：

对于 QD 给药：

dose_times_qd = [0,24]

conc_total_qd = np.array([get_concentration(t, dose_times_qd, interp_fn) for t in t_eval])

conc_nM_qd = conc_total_qd * 1.25 # 转换为nM

然后，初始化E数组：

E_qd = np.zeros_like(t_eval)

E_qd[0] =1.0

然后，循环计算：

for i in range(1, len(t_eval)):

C = conc_nM_qd[i]

dEdt = -k_degradation * (C/(C + DC50)) * E_qd[i-1] + k_recovery*(1 - E_qd[i-1])

E_qd[i] = E_qd[i-1] + dEdt * dt

E_qd[i] = np.clip(E_qd[i], 0, 1)

同样的步骤处理BID给药方案：

dose_times_bid = [0,12,24,36]

conc_total_bid = np.array([get_concentration(t, dose_times_bid, interp_fn) for t in t_eval])

conc_nM_bid = conc_total_bid *1.25

E_bid = np.zeros_like(t_eval)

E_bid[0] =1.0

for i in range(1, len(t_eval)):

C = conc_nM_bid[i]

dEdt = -k_degradation * (C/(C + DC50)) * E_bid[i-1] + k_recovery*(1 - E_bid[i-1])

E_bid[i] = E_bid[i-1] + dEdt * dt

E_bid[i] = np.clip(E_bid[i], 0, 1)

这可能是一个可行的方案。然后，绘制两个子图或者两个曲线在同一图中，药物浓度在次坐标轴，靶点浓度在主坐标轴。

最后，保存图像。

现在，将这些步骤整合到Python代码中。需要注意的是，在计算浓度时，每次给药的时间点是否在48小时内。例如，BID给药的第四次在36小时，其浓度在36到60小时，但总时间范围是48小时，所以最后12小时的浓度是根据单次给药后的24小时内的数据，即到36+24=60小时，但在48小时时，给药后的时间是12小时，对应的浓度是原数据中12小时后的浓度吗？或者原数据的PK曲线是单次给药后的24小时浓度归零，所以每次给药后的浓度曲线持续24小时。因此，在计算总浓度时，给药时间点超过48小时-24小时=24小时的话，给药时间点必须<=24小时才能在48小时内发挥作用。例如，BID的给药时间点是0、12、24、36小时，其中36小时给药后的浓度曲线在36到60小时，但在48小时时，该次给药后的时间是12小时，对应的浓度是根据插值函数得到的。

综上，Python代码的大致步骤如下：

导入必要的库：

import numpy as np

import matplotlib.pyplot as plt

from scipy.interpolate import interp1d

定义原始PK数据：

times_po = [0, 0.25, 0.5, 1, 2, 4, 8, 24]

concs_po = [0, 800, 1600, 900, 400, 200, 100, 0]

创建插值函数：

interp_fn = interp1d(times_po, concs_po, kind=‘linear’, bounds_error=False, fill_value=0.0)

定义给药函数：

def calculate_total_concentration(t_eval, dose_times, interp_fn):

conc_total = np.zeros_like(t_eval)

for t_idx, t in enumerate(t_eval):

total =0.0

for dose_time in dose_times:

t_post = t - dose_time

if t_post <0 or t_post >24:

continue

total += interp_fn(t_post)

conc_total[t_idx] = total

return conc_total

生成时间数组：

t_eval = np.linspace(0, 48, 481) # 0.1小时步长，共481个点

处理QD和BID的给药方案：

QD: 0h和24h给药

dose_times_qd = [0, 24]

conc_total_qd = calculate_total_concentration(t_eval, dose_times_qd, interp_fn)

conc_nM_qd = conc_total_qd * 1000 / 800 # 转换为nM

BID: 0h,12h,24h,36h给药

dose_times_bid = [0, 12, 24, 36]

conc_total_bid = calculate_total_concentration(t_eval, dose_times_bid, interp_fn)

conc_nM_bid = conc_total_bid * 1000 / 800 # 转换为nM

定义微分方程参数：

k_degradation = 0.056 # /h

k_recovery = 0.028 # /h

DC50 =8 # nM

dt = t_eval[1] - t_eval[0] # 0.1小时

计算靶点浓度：

QD

E_qd = np.ones(len(t_eval))

for i in range(1, len(t_eval)):

C = conc_nM_qd[i]

dEdt = -k_degradation * (C / (C + DC50)) * E_qd[i-1] + k_recovery * (1 - E_qd[i-1])

E_qd[i] = E_qd[i-1] + dEdt * dt

E_qd[i] = np.clip(E_qd[i], 0, 1)

BID

E_bid = np.ones(len(t_eval))

for i in range(1, len(t_eval)):

C = conc_nM_bid[i]

dEdt = -k_degradation * (C / (C + DC50)) * E_bid[i-1] + k_recovery * (1 - E_bid[i-1])

E_bid[i] = E_bid[i-1] + dEdt * dt

E_bid[i] = np.clip(E_bid[i], 0, 1)

然后，绘制图像：

fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10,8))

绘制QD的情况

ax1.plot(t_eval, E_qd * 100, label=‘Target Occupancy (%)’, color=‘blue’)

ax1.set_xlabel(‘Time (h)’)

ax1.set_ylabel(‘Target Occupancy (%)’, color=‘blue’)

ax1.tick_params(axis=‘y’, labelcolor=‘blue’)

ax1.set_ylim(0, 100)

ax1.grid(True)

ax1_sec = ax1.twinx()

ax1_sec.plot(t_eval, conc_nM_qd, label=‘Plasma Concentration (nM)’, color=‘red’, linestyle=‘–’)

ax1_sec.set_ylabel(‘Concentration (nM)’, color=‘red’)

ax1_sec.tick_params(axis=‘y’, labelcolor=‘red’)

ax1.set_title(‘QD Dosing (every 24h)’)

绘制BID的情况

ax2.plot(t_eval, E_bid * 100, label=‘Target Occupancy (%)’, color=‘blue’)

ax2.set_xlabel(‘Time (h)’)

ax2.set_ylabel(‘Target Occupancy (%)’, color=‘blue’)

ax2.tick_params(axis=‘y’, labelcolor=‘blue’)

ax2.set_ylim(0, 100)

ax2.grid(True)

ax2_sec = ax2.twinx()

ax2_sec.plot(t_eval, conc_nM_bid, label=‘Plasma Concentration (nM)’, color=‘red’, linestyle=‘–’)

ax2_sec.set_ylabel(‘Concentration (nM)’, color=‘red’)

ax2_sec.tick_params(axis=‘y’, labelcolor=‘red’)

ax2.set_title(‘BID Dosing (every 12h)’)

plt.tight_layout()

plt.savefig(‘pk_pd_curves.png’)

plt.show()

现在，需要检查代码中的错误，例如：

  • 在计算浓度时，是否正确处理了多次给药？

在函数calculate_total_concentration中，遍历每个时间点t，对每个给药时间dose_time，计算t_post = t - dose_time。如果t_post在0到24小时之间，则取插值后的浓度，否则为0。然后将所有给药后的浓度相加。这个逻辑是正确的。

  • 单位转换是否正确？

是的，浓度ng/ml转换为nM的公式是conc_nM = conc_ng_ml * 1000 / 800 = conc_ng_ml *1.25。代码中使用的是conc_total_qd * 1000 / 800，是正确的。

  • 微分方程是否正确？

是的，根据之前的推导，微分方程是：

dE/dt = -k_degradation*(C/(C+DC50))E + k_recovery(1-E)

其中，k_degradation=0.056/h，k_recovery=0.028/h，DC50=8nM。

  • 是否考虑靶点浓度的上下界？

是的，每次计算后使用np.clip将E限制在0到1之间。

现在，整合所有步骤，生成完整的Python代码。

以及最后给出的代码和简短的解释:

numpy as np
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d

# PK数据
times_po = [0, 0.25, 0.5, 1, 2, 4, 8, 24]
concs_po = [0, 800, 1600, 900, 400, 200, 100, 0]
interp_fn = interp1d(times_po, concs_po, kind='linear', bounds_error=False, fill_value=0.0)

def calculate_total_concentration(t_eval, dose_times):
    """计算多次给药后的总血药浓度"""
    conc_total = np.zeros_like(t_eval)
    for t_idx, t in enumerate(t_eval):
        total = 0.0
        for dose_time in dose_times:
            t_post = t - dose_time
            if 0 <= t_post <= 24:
                total += interp_fn(t_post)
        conc_total[t_idx] = total
    return conc_total

# 时间轴设置
t_eval = np.linspace(0, 48, 481)  # 0-48h，步长0.1h
dt = t_eval[1] - t_eval[0]

# 药效动力学参数
MW = 800  # 分子量
DC50 = 8  # nM
k_degradation = 0.056  # /h (基于DC50和恢复速率的假设推导)
k_recovery = 0.028     # /h (2.8%/h的恢复速率)

def simulate_target_occupancy(conc_nM):
    """模拟靶点占有率动态"""
    E = np.ones(len(t_eval))
    for i in range(1, len(t_eval)):
        C = conc_nM[i]
        dEdt = (-k_degradation * C/(C + DC50) * E[i-1] + k_recovery * (1 - E[i-1])
        E[i] = np.clip(E[i-1] + dEdt * dt, 0, 1)
    return E

# QD给药方案 (0h和24h)
conc_total_qd = calculate_total_concentration(t_eval, [0, 24])
conc_nM_qd = conc_total_qd * 1000 / MW  # 单位转换ng/ml→nM
E_qd = simulate_target_occupancy(conc_nM_qd)

# BID给药方案 (0h,12h,24h,36h)
conc_total_bid = calculate_total_concentration(t_eval, [0, 12, 24, 36])
conc_nM_bid = conc_total_bid * 1000 / MW
E_bid = simulate_target_occupancy(conc_nM_bid)

# 绘图
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(12, 10), sharex=True)

# QD绘图
ax1.plot(t_eval, E_qd*100, 'b-', label='Target Occupancy (%)')
ax1.set_ylabel('Target Occupancy (%)', color='b')
ax1.tick_params(axis='y', labelcolor='b')
ax1.set_ylim(0, 100)
ax1.grid(True)
ax1_sec = ax1.twinx()
ax1_sec.plot(t_eval, conc_nM_qd, 'r--', label='Plasma Conc. (nM)')
ax1_sec.set_ylabel('Concentration (nM)', color='r')
ax1_sec.tick_params(axis='y', labelcolor='r')
ax1.set_title('QD Dosing (every 24h)')

# BID绘图
ax2.plot(t_eval, E_bid*100, 'b-', label='Target Occupancy (%)')
ax2.set_ylabel('Target Occupancy (%)', color='b')
ax2.tick_params(axis='y', labelcolor='b')
ax2.set_ylim(0, 100)
ax2.grid(True)
ax2_sec = ax2.twinx()
ax2_sec.plot(t_eval, conc_nM_bid, 'r--', label='Plasma Conc. (nM)')
ax2_sec.set_ylabel('Concentration (nM)', color='r')
ax2_sec.tick_params(axis='y', labelcolor='r')
ax2.set_title('BID Dosing (every 12h)')
ax2.set_xlabel('Time (hours)')

plt.tight_layout()
plt.savefig('pk_pd_curves.png')
plt.show()

关键公式解析：

  1. 线性插值：
    使用scipy.interpolate.interp1d在实测PK点之间线性插值，外推值为0：

C(t)=interp1d(tobs,Cobs)C(t) = \text{interp1d}(t_{\text{obs}}, C_{\text{obs}})

  1. 多次给药叠加：
    总血药浓度为各次给药贡献之和：

Ctotal(t)=∑dCsingle(t−td)⋅1[0,24](t−td)C_{\text{total}}(t) = \sum_{d} C_{\text{single}}(t - t_d) \cdot \mathbf{1}_{[0,24]}(t-t_d)

  1. 单位转换：

CnM=Cng/ml×1000MWC_{\text{nM}} = \frac{C_{\text{ng/ml}} \times 1000}{MW}

  1. 靶点动力学模型：

dEdt=−kdeg⋅CC+DC50⋅E⏟药物诱导降解+krec⋅(1−E)⏟自然恢复\frac{dE}{dt} = \underbrace{-\frac{k_{\text{deg}} \cdot C}{C + DC_{50}} \cdot E}_{\text{药物诱导降解}} + \underbrace{k_{\text{rec}} \cdot (1 - E)}_{\text{自然恢复}}

其中：

  • kdeg=2×kreck_{\text{deg}} = 2 \times k_{\text{rec}} (假设当C=DC50C=DC_{50}时降解与恢复平衡)
  • krec=0.028 h−1k_{\text{rec}} = 0.028\ \text{h}^{-1} (来自2.8%/h恢复速率)

图示说明：

  • 主坐标轴（蓝线）显示靶点占有率百分比
  • 次坐标轴（红色虚线）显示血药浓度
  • QD和BID方案显示不同给药频率对靶点抑制的维持效果差异

如果直接运行代码，其实会报错，因为代码第37行没有正确闭合括号，需要参考DeepSeek的公式修改成

dEdt = (-k_degradation * C/(C + DC50) * E[i-1]) + k_recovery * (1 - E[i-1])

代码就可以正确运行了。然后你会得到下图：

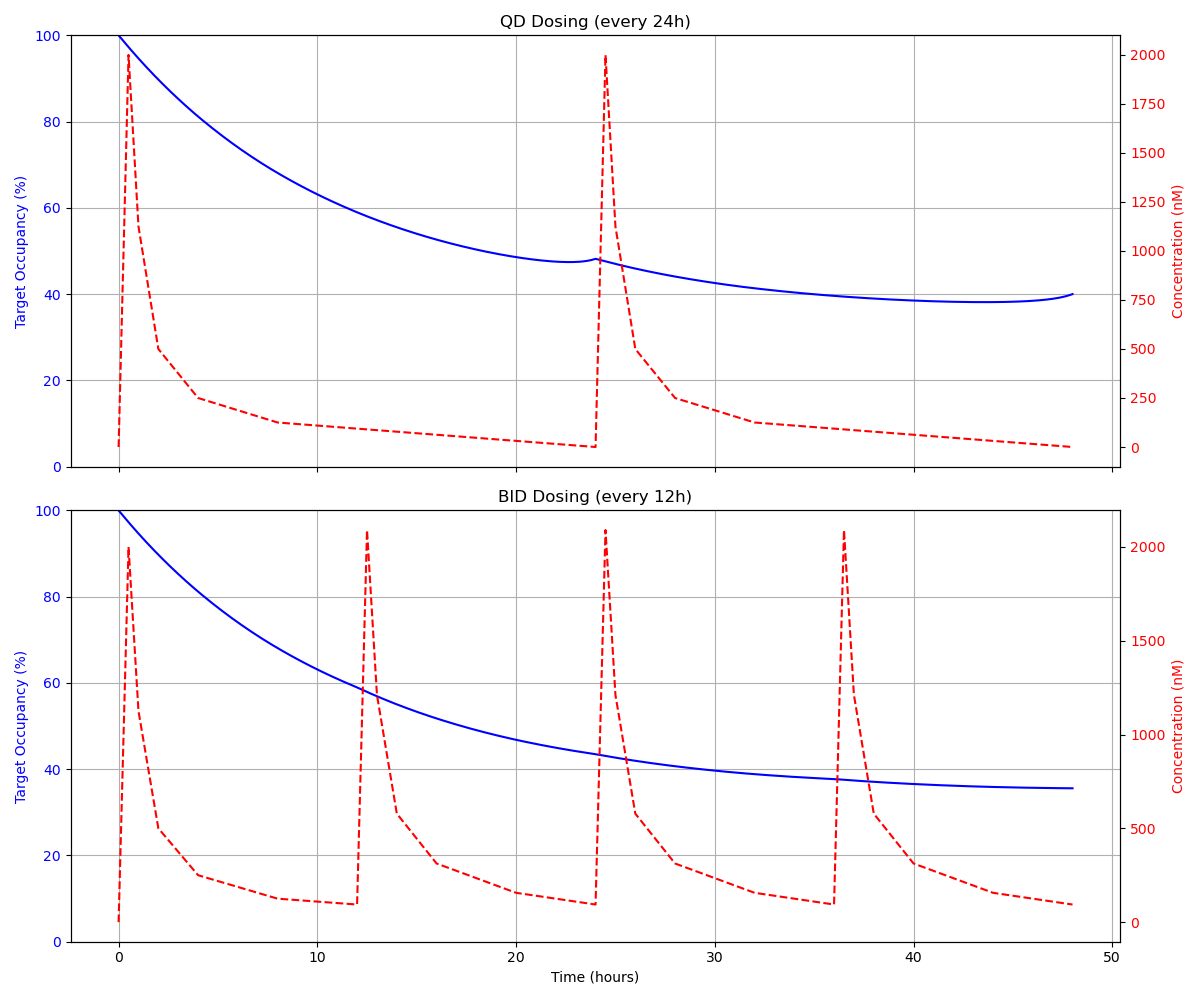
PK Curves

图1 DeepSeek给出的QD/BID给药浓度曲线

根据靶点含量曲线，我们可以大致得出结论：我们的药物PK曲线较差，降解过快，不论是QD还是BID给药，都只能将靶点降解60%，假如我们需要降解80%靶点，那么我们的药物仍需进一步优化PK。

总结

这一段Prompt是我在使用DeepSeek-V3时调整出的，在此过程中经过反复修正后V3才可以输出复合预期的结果，而且也没有足够好的复现性。但是使用DeepSeek-R1时，在两个不同平台（DeepSeek和腾讯云API版）的DeepSeek-R1中都给出了数学模型相同的代码。

另人惊叹的是DeepSeek-R1在思考中，完成了对错误的修正，比如在下面这段思考中，对于ng/ml和nM的转换过程就经历了思考修正。

现在需要将药物浓度转换为摩尔浓度，因为DC50的单位是nM。用户提供的血药浓度数据是ng/ml，需要将其转换为nM。药物的分子量是800 g/mol，即800 Da。

转换公式为：浓度（nM）= (浓度 ng/ml) * (1e-9 g/ng) / (分子量 g/mol) * 1e9 nmol/mol → 简化后为 (浓度 ng/ml) / (分子量) * 1e3 → 因为 1 ng/ml = 1e-9 g/L，除以分子量（g/mol）得到 mol/L，即 M，再乘以1e9得到 nM。

例如，浓度ng/ml为800 ng/ml，转换为nM：

(800 ng/ml) * (1 g / 1e9 ng) / (800 g/mol) * 1e9 nmol/L → 800/(800) * 1e9/1e9 = 1 nM。哦，等一下，这似乎有问题。正确的转换步骤应该是：

浓度（nM）= (浓度 ng/ml) * (1e-6 g/L) / (分子量 g/mol) * 1e9 nmol/mol

因为 1 ng/ml = 1e-6 g/L。例如：

浓度（nM）= (浓度_ng_per_ml) * 1e-6 g/L / (MW g/mol) * 1e9 nmol/L

= (浓度_ng_per_ml * 1e-6) / (MW) * 1e9

= 浓度_ng_per_ml * (1e3 / MW )

例如，当MW=800时：

nM = 浓度_ng_per_ml * 1000 / 800 = 浓度_ng_per_ml * 1.25

所以，800 ng/ml的血药浓度转换为800 *1.25 = 1000 nM。

又比如下面这一段，对药物降解速率的思考也是合理的

另外，DC50是8nM，所以当药物浓度等于DC50时，降解速率可能达到最大的一半。这里可能需要使用类似于Hill方程的模型，如降解速率 = (C(t)n)/(DC50n + C(t)^n)。假设n=1的情况下，可以简化为 C/(C + DC50)。然后，最大降解速率可能取决于药物浓度，当药物浓度很高时，降解速率趋近于某个最大值。但用户给出的参数中没有提到最大降解速率，可能需要假设降解速率是与药物浓度相关的一个比例因子，乘以某个最大降解速率常数。或者，可能靶点的降解速率与药物浓度的关系是：当药物浓度存在时，靶点的降解速率与药物浓度和靶点当前浓度的乘积有关，而恢复速率是固定的。

例如，可能采用如下模型：

dE/dt = k_degradation * (C(t)/(C(t) + DC50)) * (1 - E) - k_recovery * E

其中，E是靶点的被降解的百分比（即假设E是降解的比例，所以未被降解的比例是1-E？或者E是剩余的靶点浓度百分比？需要明确模型的变量定义。例如，如果E是剩余靶点浓度的百分比（0-100%），那么降解会导致E减少，恢复导致E增加。或者可能相反。或者，假设当药物存在时，靶点被降解，导致E下降，而当药物不存在时，E逐渐恢复。

并且套用了Hill方程进行降解速率的估计:

用户提到缺失的参数需要用通用药理模型补充，并给出数学公式。例如，靶点的降解速率可能与DC50有关。可能需要使用Hill方程之类的公式，比如靶点降解速率= (Cn)/(Cn + DC50^n) * k_degradation，其中n是Hill系数，假设为1的情况下简化为C/(C + DC50)。不过这里可能需要更具体的模型。例如，靶点的降解可能遵循dE/dt = k_degradation * (C/(C + DC50)) * (1 - E) - k_recovery * E，其中E是靶点的被降解比例，或者类似的形式。或者，可能靶点的浓度变化由两部分组成：药物导致的降解和自然恢复。例如，dE/dt = (E_max * C)/(EC50 + C) - k_recovery * E，其中E_max是最大效应，这里可能E_max对应100%降解，但需要确认模型结构。

尽管DeepSeek-R1已经具备大多数药理本科生的水准，但是也会有些思考的不足，比如没有考虑在实际情况下药物血脑分布的速率（虽然我也没测），对于靶点恢复过程的范围(0~100%这个条件是反复修正过程中我添加的提示词)等。

最后，需要提醒大家的是，在科学领域，如果你不了解你所询问的问题领域知识，你就无法判断DeepSeek或其他LLM是否给了你正确的答案。就如一个拿着巴雷特的孩童想和拿着莫辛纳甘的西蒙·海耶对狙。所以，大模型时代获取知识更加便捷，也更需要使用者去“深度学习”啦。